题目内容
3.已知椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,并且直线y=x+b是抛物线C2:y2=4x的一条切线.(Ⅰ)求椭圆C1的方程.
(Ⅱ)设点A,B分别是椭圆C1的左右顶点,F是椭圆C1的左焦点.若过点P(-2,0)的直线与椭圆C1相交于不同两点M,N.
①求证:∠AFM=∠BFN;②求△MFN面积的最大值.
分析 (Ⅰ)将直线方程代入抛物线方程,由△=0,即可求得b的值,由椭圆的离心率公式,即可求得a的值,即可求得椭圆C1的方程;
(Ⅱ)①由:当MN斜率为0时,显然∠AFM=∠BFN=0满足题意;当直线MN的斜率不为0时,设直线l的方程,代入椭圆方程,利用韦达定理及直线的斜率公式,即可求得kMF=kNF,则∠AFM=∠BFN;
②由①可知:根据弦长公式及三角形的面积公式,根据基本不等式的性质,即可求得△MFN面积的最大值.
解答 解:(Ⅰ)由$\left\{\begin{array}{l}y=x+b\\{y^2}=4x\end{array}\right.$,得:x2+(2b-4)x+b2=0,由y=x+b是抛物线C2的一条切线,
∴△=(2b-4)2-4b2=0,得b=1,
由e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{{\sqrt{2}}}{2}$,可得 $a=\sqrt{2}$.
∴椭圆C1的方程为:$\frac{x^2}{2}+{y^2}=1$.
(Ⅱ)①证明:当MN斜率为0时,显然∠AFM=∠BFN=0满足题意;
当MN斜率不为0时,设M(x1,y1),N(x2,y2),MN的方程为:x=my-2
$\left\{\begin{array}{l}{x=my-2}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,整理得:(m2+2)y2-4my+2=0,
则∴△=16m2-8(m2+2)=8m2-16>0,
∴m2>2,
${y_1}+{y_2}=\frac{4m}{{{m^2}+2}},{y_1}{y_2}=\frac{2}{{{m^2}+2}}$,
所以,${k_{MF}}+{k_{NF}}=\frac{y_1}{{{x_1}+1}}+\frac{y_2}{{{x_2}+1}}=\frac{y_1}{{m{y_1}-1}}+\frac{y_2}{{m{y_2}-1}}$=$\frac{{2m{y_1}{y_2}-({y_1}+y_2^{\;})}}{{(m{y_1}-1)(m{y_2}-1)}}=\frac{{2m•\frac{2}{{{m^2}+2}}-\frac{4m}{{{m^2}+2}}}}{{(m{y_1}-1)(m{y_2}-1)}}=0$,即∠AFM=∠BFN.
②${S_{△MNF}}=|{{S_{△PNF}}-{S_{△PMF}}}|=\frac{1}{2}|{PF}||{{y_1}-{y_2}}|$=$\frac{1}{2}×1×\frac{{\sqrt{8{m^2}-16}}}{{{m^2}+2}}=\frac{{\sqrt{2({m^2}-2)}}}{{({m^2}-2)+4}}$=$\frac{{\sqrt{2}}}{{\sqrt{{m^2}-2}+\frac{4}{{\sqrt{{m^2}-2}}}}}≤\frac{{\sqrt{2}}}{4}$,
当且仅当 $\sqrt{{m^2}-2}=\frac{4}{{\sqrt{{m^2}-2}}}$,即m2=6时取等号.
∴△MNF面积最大值是$\frac{{\sqrt{2}}}{4}$.
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查韦达定理,弦长公式,直线的斜率公式及基本不等式的应用,考查计算能力,属于中档题.

 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案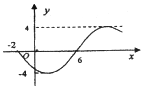
| A. | y=-4sin($\frac{π}{8}$x-$\frac{π}{4}$) | B. | y=-4sin($\frac{π}{8}$x+$\frac{π}{4}$) | C. | y=4sin($\frac{π}{8}$x-$\frac{π}{4}$) | D. | y=4sin($\frac{π}{8}$x+$\frac{π}{4}$) |
| A. | (0,2] | B. | (0,$\frac{1}{2}$] | C. | [$\frac{1}{2}$,2] | D. | [2,+∞) |
| A. | $\frac{1}{3}$ | B. | 3 | C. | -3 | D. | -$\frac{1}{3}$ |
 某程序框图如图,该程序运行后输出的k值是( )
某程序框图如图,该程序运行后输出的k值是( )| A. | 3 | B. | 4 | C. | 6 | D. | 8 |