题目内容
5.在△ABC中,内角A,B,C所对的边分别是a,b,c,已知$csinA=\sqrt{3}acosC$,(a-c)(a+c)=b(b-c),函数$f(x)=2sinxcos(\frac{π}{2}-x)-\sqrt{3}sin(π+x)cosx+sin(\frac{π}{2}+x)cosx$(1)求函数y=f(x)的周期和对称轴方程;
(2)求f(B)的值.
分析 (1)利用诱导公式,二倍角以及辅助角公式基本公式将函数化为y=Asin(ωx+φ)的形式,再利用周期公式求函数的最小正周期,结合三角函数的图象和性质,可得对称轴方程
(2)利用正余弦定理求解出A,B的角的大小即可求出f(B)的值.
解答 解:函数$f(x)=2sinxcos(\frac{π}{2}-x)-\sqrt{3}sin(π+x)cosx+sin(\frac{π}{2}+x)cosx$,
化简可得:$f(x)=2{sin^2}x+\sqrt{3}sinxcosx+{cos^2}x={sin^2}x+\sqrt{3}sinxcosx+1$=$\frac{1-cos2x}{2}+\frac{{\sqrt{3}}}{2}sin2x+1=sin({2x-\frac{π}{6}})+\frac{3}{2}$,
(1)∴函数f(x)的周期T$\frac{2π}{2}$═π.
对称轴方程:令$2x-\frac{π}{6}=\frac{π}{2}+kπ,k∈Z,则x=\frac{π}{3}+\frac{kπ}{2},k∈Z$.
故对称轴方程为$x=\frac{π}{3}+\frac{kπ}{2},k∈Z$.
(2)∵$csinA=\sqrt{3}acosC$,
正弦定理,得:$sinCsinA=\sqrt{3}sinAcosC$,
化简得$tanC=\sqrt{3}$,
∵0<C<π,
∴$C=\frac{π}{3}$,
又∵(a-c)(a+c)=b(b-c),
可得:a2=b2+c2-bc=b2+c2-2bccosA,
∴cosA=$\frac{1}{2}$,
∵0<A<π,
得:$A=\frac{π}{3}$,
故$B=π-A-C=\frac{π}{3}$.
∴$f(B)=sin({\frac{2π}{3}-\frac{π}{6}})+\frac{3}{2}=\frac{5}{2}$.
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用三角函数公式将函数进行化简是解决本题的关键.同时考查了正余弦定理的运用和计算能力.属于中档题.

| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
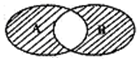 如图所示的韦恩图中,A、B是非空集合,定义A*B表示阴影部分的集合.若x,y∈R,A={x|y=$\sqrt{2x-{x}^{2}}$},B={y|y=3x,x>0}.则A*B为( )
如图所示的韦恩图中,A、B是非空集合,定义A*B表示阴影部分的集合.若x,y∈R,A={x|y=$\sqrt{2x-{x}^{2}}$},B={y|y=3x,x>0}.则A*B为( )| A. | {x|0<x<2} | B. | {x|1<x≤2} | C. | {x|0≤x≤1或x≥2} | D. | {x|0≤x≤1或x>2} |
| A. | 是奇函数,且在(-∞,+∞)上是减函数 | B. | 是偶函数,且在(-∞,+∞)上是减函数 | ||
| C. | 是偶函数,且在(-∞,+∞)上是增函数 | D. | 是奇函数,且在(-∞,+∞)上是增函数 |
| A. | y=sinx | B. | y=sin2|x| | C. | y=-cos2x | D. | y=cos2x |
 如果执行右边的程序框图,输出的值为x,则${x}^{\frac{1}{2}}$+log3x=5.
如果执行右边的程序框图,输出的值为x,则${x}^{\frac{1}{2}}$+log3x=5.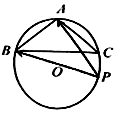 如图,在△A BC中,三内角 A,B,C的对边分别为a,b,c,且a2=b2+c2+bc,$a=\sqrt{3}$,S为△A BC的面积,圆 O是△A BC的外接圆,P是圆 O上一动点,
如图,在△A BC中,三内角 A,B,C的对边分别为a,b,c,且a2=b2+c2+bc,$a=\sqrt{3}$,S为△A BC的面积,圆 O是△A BC的外接圆,P是圆 O上一动点,