题目内容
9.定义区间(c,d)、(c,d]、[c,d)、[c,d]的长度均为d-c(d>c),己知实数p>0,则满足不等式$\frac{1}{x-p}$+$\frac{1}{x}$≥1的x构成的区间长度之和为2.分析 原不等式化为$\frac{{x}^{2}-(p+2)x+p}{x(x-p)}$≤0,设x2-(p+2)x+p=0的根为x1和x2,则由求根公式可得这两个根的值,结合数轴,用穿根法来解的不等式的解集,从而求得解集构成的区间的长度之和.
解答 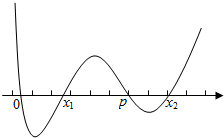 解:∵$\frac{1}{x-p}$+$\frac{1}{x}$≥1,实数p>0,∴$\frac{2x-p}{x(x-p)}$≥1,即$\frac{{x}^{2}-(p+2)x+p}{x(x-p)}$≤0,
解:∵$\frac{1}{x-p}$+$\frac{1}{x}$≥1,实数p>0,∴$\frac{2x-p}{x(x-p)}$≥1,即$\frac{{x}^{2}-(p+2)x+p}{x(x-p)}$≤0,
设x2-(p+2)x+p=0的根为x1和x2,则由求根公式可得,
x1=$\frac{p+2-\sqrt{{p}^{2}+4}}{2}$,x2=$\frac{p+2+\sqrt{{p}^{2}+4}}{2}$,
把不等式的根排在数轴上,
由穿根得不等式的解集为(0,x1)∪(p,x2 ),故解集构成的区间的长度之和为 (x1-0)+(x2-p )
=(x1+x2 )-p=(p+2)-p=2,
故答案为:2.
点评 本题考查其他不等式的解法,解题的关键是掌握用穿根法解分式不等式和高次不等式的技巧,本题中令分子为0,得出x1和x2与系数的关系对解本题尤其关键.本题考查数形结合的思想,是不等式求解中难度较大的题型.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
19.△ABC的两个顶点为A(-1,0),B(1,0),△ABC周长为6,则C点轨迹方程为( )
| A. | $\frac{x^2}{4}+\frac{y^2}{3}=1$(y≠0) | B. | $\frac{y^2}{4}+\frac{x^2}{3}=1$(y≠0) | C. | $\frac{x^2}{5}+\frac{y^2}{4}=1$(y≠0) | D. | $\frac{y^2}{5}+\frac{x^2}{4}=1$(y≠0) |
17.设a=3log${\;}_{\frac{1}{3}}$2,b=3log${\;}_{\frac{1}{2}}$$\frac{1}{3}$,c=$\sqrt{\frac{2}{3}}$,则下列结论正确的是( )
| A. | a<b<c | B. | a<c<b | C. | b<a<c | D. | b<c<a |