题目内容
17.设a=3log${\;}_{\frac{1}{3}}$2,b=3log${\;}_{\frac{1}{2}}$$\frac{1}{3}$,c=$\sqrt{\frac{2}{3}}$,则下列结论正确的是( )| A. | a<b<c | B. | a<c<b | C. | b<a<c | D. | b<c<a |
分析 利用对数函数的性质,即可比较.
解答 解:a=3log${\;}_{\frac{1}{3}}$2<0,b=3log${\;}_{\frac{1}{2}}$$\frac{1}{3}$>3log${\;}_{\frac{1}{2}}$$\frac{1}{2}$=3,0<$\sqrt{\frac{2}{3}}$<1,
∴a<c<b,
故选:B.
点评 本题考查了对数函数的大小比较,关键是掌握对数函数的性质,属于基础题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
12.函数f(x)=sin2(2x+$\frac{π}{3}$)的导数是( )
| A. | f′(x)=2sin(2x+$\frac{π}{3}$) | B. | f′(x)=4sin(2x+$\frac{π}{3}$) | C. | f′(x)=sin(4x+$\frac{2π}{3}$) | D. | f′(x)=2sin(4x+$\frac{2π}{3}$) |
17.(x+8)(3-x)<0的一个充分不必要条件是( )
| A. | -8<x<3 | B. | x>8 | C. | x<-3 | D. | x<-8或x>3 |
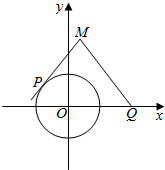 已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1.动点M到圆的切线长等于|MQ|的2倍.
已知直角坐标平面上点Q(2,0)和圆C:x2+y2=1.动点M到圆的切线长等于|MQ|的2倍.