题目内容
 四个幂函数y=xa;y=xb;y=xc;y=xd在同一坐标系中的图象如图所示,则a,b,c,d,0,1由大到小的顺序是
四个幂函数y=xa;y=xb;y=xc;y=xd在同一坐标系中的图象如图所示,则a,b,c,d,0,1由大到小的顺序是考点:幂函数的图像
专题:函数的性质及应用
分析:根据幂函数的图象和性质,即可判断幂指数的大小.
解答:
解:①y=xa,单调递增,且当x>1时,在直线y=x的上方,∴a>1,
②y=xb,单调递增,且当x>1时,在直线y=x的下方,∴0<b<1,
③y=xc,单调递减,且当x>1时,在直线y=x的下方,∴c<0,
④y=xd,单调递减,且当x>1时,在直线y=x的下方,∴d<0,
当x=2时,2a>2b>2c>2d,
∴a>b>c>d,
即a,b,c,d,0,1由大到小的顺序是a>1>b>0>c>d,
故答案为:a>1>b>0>c>d.
②y=xb,单调递增,且当x>1时,在直线y=x的下方,∴0<b<1,
③y=xc,单调递减,且当x>1时,在直线y=x的下方,∴c<0,
④y=xd,单调递减,且当x>1时,在直线y=x的下方,∴d<0,
当x=2时,2a>2b>2c>2d,
∴a>b>c>d,
即a,b,c,d,0,1由大到小的顺序是a>1>b>0>c>d,
故答案为:a>1>b>0>c>d.
点评:本题主要考查幂函数的图象和性质,利用函数的单调性以及特殊值法是解决本题的关键,比较基础.

练习册系列答案
相关题目
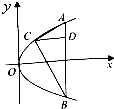 如图,直角三角形ABC的三个顶点在给定的抛物线y2=2px(p>0)上,斜边AB平行于y轴,则AB边上的高|CD|=
如图,直角三角形ABC的三个顶点在给定的抛物线y2=2px(p>0)上,斜边AB平行于y轴,则AB边上的高|CD|=