题目内容
已知下列等式:
12=1
12-32+52=17
12-32+52-72+92=49
12-32+52-72+92-112+132=97
观察上式的规律,写出第n个等式 .
12=1
12-32+52=17
12-32+52-72+92=49
12-32+52-72+92-112+132=97
观察上式的规律,写出第n个等式
考点:归纳推理
专题:规律型
分析:等式的左边是正奇数的平方和或差,根据这一规律得第n个等式左边为12-32+52-72+…-(4n-5)2+(4n-3)2.利用平方差公式展开后,结合数列求和的方法,可得答案.
解答:
解:观察下列等式:
12=1
12-32+52=17
12-32+52-72+92=49
12-32+52-72+92-112+132=97
…
归纳可得第n个等式为:
12-32+52-72+…-(4n-5)2+(4n-3)2
=1+2(3+5)+2(7+9)+…+2[(4n-5)+(4n-3)]
=1+2[3+5+7+9+…+(4n-5)+(4n-3)]
=1+2×
=8n2-8n+1.
故答案为:12-32+52-72+…-(4n-5)2+(4n-3)2=8n2-8n+1
12=1
12-32+52=17
12-32+52-72+92=49
12-32+52-72+92-112+132=97
…
归纳可得第n个等式为:
12-32+52-72+…-(4n-5)2+(4n-3)2
=1+2(3+5)+2(7+9)+…+2[(4n-5)+(4n-3)]
=1+2[3+5+7+9+…+(4n-5)+(4n-3)]
=1+2×
| 2(n-1)(3+4n-3) |
| 2 |
=8n2-8n+1.
故答案为:12-32+52-72+…-(4n-5)2+(4n-3)2=8n2-8n+1
点评:本题考查规律型中的数字变化问题,找等式的规律时,既要分别看左右两边的规律,还要注意看左右两边之间的联系.

练习册系列答案
相关题目
已知a=log23+log2
,b=log23
,c=log32,则a,b,c的大小关系是( )
| 3 |
| 3 |
| A、a=b>c |
| B、a=b<c |
| C、a<b<c |
| D、a>b>c |
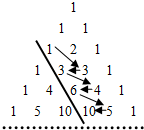 如图,在杨辉三角中,斜线l的上方从1按箭头方向可以构成一个“锯齿形”的数列{an}:1,3,3,4,6,5,10,…,记其前n项和为Sn,则S27的值为
如图,在杨辉三角中,斜线l的上方从1按箭头方向可以构成一个“锯齿形”的数列{an}:1,3,3,4,6,5,10,…,记其前n项和为Sn,则S27的值为 一个街区有南北走向6条街和东西走向5条街,某人从街道的西北角A点走到东南角B点,最短的走法有
一个街区有南北走向6条街和东西走向5条街,某人从街道的西北角A点走到东南角B点,最短的走法有