题目内容
如图，已知A（4，0），B（0，4），P（t，0）（0＜t＜4），光源P发出的光线设在AB上的Q处反射在OB上的R处，最后反射在P处．①若t=2，则PQ+QR+RP= ；②若QR过△ABO的重心，则t= ．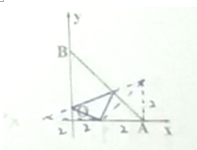
考点：向量在几何中的应用
专题：平面向量及应用
分析：如图，根据对称的知识可知，PQ=QN，PR=RM，所以所求的长度即为MN的长度，可以先求出M，N的坐标，然后利用两点间的距离公式计算即可；若QR过△ABO的重心，由已知容易求得重心的坐标，代入MN的直线方程，即可求出t的值．
解答：
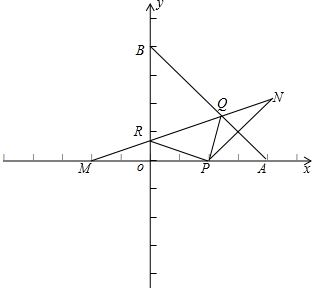解：如图所示：由已知设P（t，0），且A（4，0），B（0，4），M（-t，0），
因为P，N关于AB对称，所以N（4，4-t），
又根据对称得PQ=QN，PR=MR，所以PQ+QR+RP=MN=
=
．
当t=2时，代入上式得MN=2
．
根据已知得kMN=
，故直线MN的方程为y=
(x+t)．
而△ABO的重心为（
，
），代入MN的方程得t=
．
故答案为：2
；
．
解：如图所示：由已知设P（t，0），且A（4，0），B（0，4），M（-t，0），因为P，N关于AB对称，所以N（4，4-t），
又根据对称得PQ=QN，PR=MR，所以PQ+QR+RP=MN=
| (4+t)2+(4-t)2 |
| 32+2t2 |
当t=2时，代入上式得MN=2
| 10 |
根据已知得kMN=
| 4-t |
| 4+t |
| 4-t |
| 4+t |
而△ABO的重心为（
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
故答案为：2
| 10 |
| 4 |
| 3 |
点评：本题考查了坐标法解决几何问题的基本思路，本题的关键是根据对称表示出点M，N的坐标．
练习册系列答案
相关题目
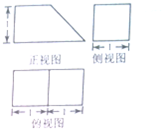
某几何体的三视图如图所示，则该几何体的体积胃（ ）
A、1+
| ||||
B、3+
| ||||
C、
| ||||
| D、3 |
矩形ABCD满足AB=2，AD=1，点A、B分别在射线OM，ON上，∠MON为直角，当C到点O的距离最大时，∠BAO的大小为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知数列{an}满足a1=2，（n+1）•an+1=2（n+2）•an，若数列{an}的前n项和为Sn，则
=（ ）
| an+1 |
| Sn |
A、
| ||
B、
| ||
C、
| ||
D、
|