题目内容
在△ABC中,∠BAC=120°,AD为角分线,AC=3,AB=6,AD为 .
考点:余弦定理的应用
专题:解三角形
分析:由AD为内角A的平分线,利用角平分线定义得到∠BAD=∠CAD=60°,根据三角形ABD面积+三角形ACD面积=三角形ABC面积,利用三角形面积公式求出AD的长即可.
解答:
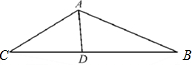 解:∵AD是△ABC的内角A的平分线,且∠BAC=120°,AC=3,AB=6,
解:∵AD是△ABC的内角A的平分线,且∠BAC=120°,AC=3,AB=6,
∴∠BAD=∠CAD=60°,
∵S△ABD+S△CAD=S△ABC,
∴
AB•ADsin∠ABD+
AC•ADsin∠CAD=
AB•ACsin∠BAC,
即
×3AD×
+
×6AD×
=
×3×6×
,
解得:AD=2,
故答案为:2.
 解:∵AD是△ABC的内角A的平分线,且∠BAC=120°,AC=3,AB=6,
解:∵AD是△ABC的内角A的平分线,且∠BAC=120°,AC=3,AB=6,∴∠BAD=∠CAD=60°,
∵S△ABD+S△CAD=S△ABC,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
解得:AD=2,
故答案为:2.
点评:此题考查三角形面积公式,也可以利用余弦定理求解AD,以及熟练掌握三角形面积公式是解本题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
已知抛物线y2=4px(p>0)与双曲线
-
=1(a>0,b>0)有相同的焦点F,点A是两个曲线的一个交点,O为坐标原点,且OA=FA,则双曲线的离心率的平方为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、2 | ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|