题目内容
7.设△ABC的内角A、B、C的对边长分别为a、b、c,若bsinB-csinC=a,且△ABC的面积S=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{4}$,则B=77.5°.分析 利用余弦定理、正弦定理、三角形的面积公式,结合二倍角公式,即可求出B.
解答 解:在△ABC中,∵S=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{4}$,
∴$\frac{1}{2}$bcsinA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{4}$,
∴$\frac{1}{2}$bcsinA=$\frac{1}{2}$bccosA,
∴tanA=1,
∴A=45°
∵bsinB-csinC=a,
∴sin2B-sin2C=$\frac{\sqrt{2}}{2}$,
∴cos2C-cos2B=$\frac{\sqrt{2}}{2}$,
∴cos(270°-2B)-cos2B=$\frac{\sqrt{2}}{2}$,
∴-sin2B-cos2B=$\frac{\sqrt{2}}{2}$,
∴sin(2B+45°)=-$\frac{1}{2}$,
∴2B+45°=210°或2B+45°=330°,
∴B=77.5°或142.5°(舍去).
故答案为:77.5°.
点评 本题考查余弦定理、正弦定理、三角形的面积公式、二倍角公式,考查学生的计算能力,正确转化是关键.

练习册系列答案
相关题目
18.数列2014,2015,1,-2014,…;从第二项起,每一项都等于它的前后两项之和,则该数列的前2015项之和等于( )
| A. | 2014 | B. | 2015 | C. | 1 | D. | 0 |
2.若平面α外的直线l的方向向量为$\overrightarrow{a}$,平面α的法向量为$\overrightarrow{u}$,则能使l∥α的是( )
| A. | $\overrightarrow{a}$=(1,-3,5),$\overrightarrow{u}$=(1,0,1) | B. | $\overrightarrow{a}$=(1,0,0),$\overrightarrow{u}$=(-2,0,0) | ||
| C. | $\overrightarrow{a}$=(0,2,1),$\overrightarrow{u}$=(-1,0,1) | D. | $\overrightarrow{a}$=(1,-1,3),$\overrightarrow{u}$=(0,3,1) |
12.在空间直角坐标系O-xyz中,一个四面体的顶点坐标分别是(0,0,2),(2,0,0),(2,1,1),(0,1,1).若画该四面体三视图时,正视图以zOy平面为投影面,则得到的侧视图是( )
| A. |  | B. | 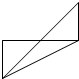 | C. | 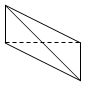 | D. | 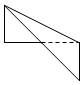 |
19.已知复数z=i(1+i),则|z|等于( )
| A. | 0 | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
16.已知函数f(x)=$\left\{\begin{array}{l}\frac{x}{3},0≤x≤\frac{1}{2}\\ \frac{{2{x^3}}}{x+1},\frac{1}{2}<x≤1\end{array}$,若函数g(x)=ax-$\frac{a}{2}$+3(a>0),若对?x1∈[0,1],总?x2∈[0,$\frac{1}{2}$],使得f(x1)=g(x2)成立,则实数a的取值范围是( )
| A. | (-∞,6] | B. | [6,+∞) | C. | (-∞,-4] | D. | [-4,+∞) |
17.若实数x,y满足不等式组$\left\{\begin{array}{l}{|x-1|≤1}\\{y≥0}\\{y≤x+1}\end{array}\right.$,则下列结论中正确的是( )
| A. | 2x-y≥0 | B. | 2x-y≤3 | C. | x+y≤6 | D. | x+y<2 |