题目内容
12．在空间直角坐标系O-xyz中，一个四面体的顶点坐标分别是（0，0，2），（2，0，0），（2，1，1），（0，1，1）．若画该四面体三视图时，正视图以zOy平面为投影面，则得到的侧视图是（ ）| A． |  | B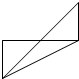． |  | C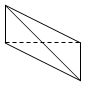． |  | D． |  |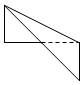
分析 由题意，利用空间直角坐标系，借助于正方体在坐标系中画出几何体，再画出它的侧视图．
解答 
解：由题意，画出直角坐标系，在坐标系中各点对应位置如图①所示；
以平面zOy为投影面，得到的侧视图如图②所示：
故选：C．
点评 本题考查了空间几何体的三视图与应用问题，解题的关键是有丰富的空间想象能力．
练习册系列答案
走进文言文系列答案
相关题目
3．已知$\overrightarrow a$=（1，1，1），$\overrightarrow b$=（0，y，1）（0≤y≤1），则cos＜$\overrightarrow a$，$\overrightarrow b$＞最大值为（ ）
| A． | $\frac{{\sqrt{3}}}{3}$ | B． | $\frac{{\sqrt{2}}}{3}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | $\frac{{\sqrt{6}}}{3}$ |