题目内容
已知f(x)=
,若f(x)=3,则x的值为( )
|
|
A、1或
| ||||
B、±
| ||||
C、
| ||||
D、1或±
|
考点:分段函数的应用
专题:函数的性质及应用
分析:根据分段函数的表达式分别进行求解即可.
解答:
解:若x≤-1,由f(x)=3得f(x)=x+2=3,解得x=1,不满足条件,
若-1<x<2,由f(x)=3得f(x)=x2=3,解得x=
或-
(舍),故x=
满足条件,
若x≥2,由f(x)=3得f(x)=2x=3,解得x=
,不满足条件,
综上x=
,
故选:C.
若-1<x<2,由f(x)=3得f(x)=x2=3,解得x=
| 3 |
| 3 |
| 3 |
若x≥2,由f(x)=3得f(x)=2x=3,解得x=
| 3 |
| 2 |
综上x=
| 3 |
故选:C.
点评:本题主要考查函数值的求解,根据分段函数的表达式分别进行求解是解决本题的关键.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
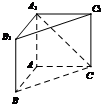 如图,直三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC.若AB=AC=AA1=1,BC=
如图,直三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC.若AB=AC=AA1=1,BC=| 2 |
| A、30° | B、45° |
| C、60° | D、90° |
若关于x的方程x2-3x+a=0和x2-3x+b=0(a≠b)的四个根可组成首项为6的等差数列,则a+b的值是( )
| A、-18 | B、9 | C、-3 | D、-3 |