题目内容
求函数y=lgx+lg（2-x）的最大值 ．
考点：复合函数的单调性
专题：函数的性质及应用
分析：先求函数的定义域，结合复合函数的性质进行求解即可．
解答：
解：由
得
，解得0＜x＜2，
则y=lgx+lg（2-x）=lgx（2-x），
设t=x（2-x），
则t=-x2+2x=-（x-1）2+1∈（0，1]，
故当t=1时，函数取得最大值为lg1=0，
故答案为：0．
|
|
则y=lgx+lg（2-x）=lgx（2-x），
设t=x（2-x），
则t=-x2+2x=-（x-1）2+1∈（0，1]，
故当t=1时，函数取得最大值为lg1=0，
故答案为：0．
点评：本题主要考查函数的最值的求解，根据对数的性质结合复合函数之间的关系是解决本题的关键．
练习册系列答案
相关题目
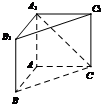如图，直三棱柱ABC-A1B1C1中，侧棱AA1⊥平面ABC．若AB=AC=AA1=1，BC=| 2 |
| A、30° | B、45° |
| C、60° | D、90° |