题目内容
16.已知sinθ、cosθ是关于x的方程x2-2$\sqrt{2}$ax+a=0的两个根.(1)求实数a的值;
(2)若θ∈(-$\frac{π}{2}$,0),求sinθ-cosθ的值.
分析 (1)由sinθ、cosθ为已知方程的两根,得到根的判别式大于等于0,求出θ的范围,利用韦达定理表示出sinθ+cosθ与sinθcosθ,利用同角三角函数间的基本关系列出关于a的方程,求出方程的解得到a的值.
(2)利用角的范围可得:sinθ<0,cosθ>0,由(1)可得:a=-$\frac{1}{4}$,sinθ+cosθ=-$\frac{\sqrt{2}}{2}$,sinθcosθ=-$\frac{1}{4}$,
从而利用sinθ-cosθ=-$\sqrt{1-2sinθcosθ}$即可求值.
解答 解:(1)∵sinθ、cosθ是方程x2-2$\sqrt{2}$ax+a=0的两个实根,
∴sinθ+cosθ=2$\sqrt{2}a$①,sinθcosθ=a②,△=b2-4ac=8a2-4a≥0,即a≤0或a≥$\frac{1}{2}$,
∴(sinθ+cosθ)2=1+2sinθcosθ=1+2a=8a2,即8a2-2a-1=0,
解得:a=-$\frac{1}{4}$,或$\frac{1}{2}$.
(2)∵θ∈(-$\frac{π}{2}$,0),
∴sinθ<0,cosθ>0,可得:sinθcosθ=a<0,由(1)可得:a=-$\frac{1}{4}$,
∴sinθ+cosθ=-$\frac{\sqrt{2}}{2}$,sinθcosθ=-$\frac{1}{4}$,
∴sinθ-cosθ=-$\sqrt{1-2sinθcosθ}$=-$\frac{\sqrt{6}}{2}$.
点评 此题考查了二倍角的正弦函数公式,以及韦达定理的应用,熟练掌握公式是解本题的关键,属于中档题.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
4.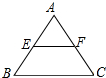 在三角形ABC中,E、F分别是AB、AC的中点,若在三角形内部,随机取一点Q,则点Q取自△AEF内部的概率是( )
在三角形ABC中,E、F分别是AB、AC的中点,若在三角形内部,随机取一点Q,则点Q取自△AEF内部的概率是( )
 在三角形ABC中,E、F分别是AB、AC的中点,若在三角形内部,随机取一点Q,则点Q取自△AEF内部的概率是( )
在三角形ABC中,E、F分别是AB、AC的中点,若在三角形内部,随机取一点Q,则点Q取自△AEF内部的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
3.已知平面α截一球面得圆M,过圆心M且与α成30°二面角的平面β截该球面得圆N.若该球面的半径为4,圆M的面积为4π,则圆N的面积为( )
| A. | 7π | B. | 9π | C. | 11π | D. | 13π |