题目内容
4.已知sin(α-π)=$\frac{2}{3}$,且$α∈(-\frac{π}{2},0)$,则tanα=-$\frac{2\sqrt{5}}{5}$.分析 利用诱导公式可求sinα=-$\frac{2}{3}$,根据同角三角函数基本关系式即可可求cosα,tanα的值.
解答 解:∵sin(α-π)=$\frac{2}{3}$,且$α∈(-\frac{π}{2},0)$,
∴sinα=-$\frac{2}{3}$,cosα=$\sqrt{1-si{n}^{2}α}$=$\frac{\sqrt{5}}{3}$,
∴$tanα=\frac{sinα}{cosα}$=-$\frac{2\sqrt{5}}{5}$.
故答案为:-$\frac{2\sqrt{5}}{5}$.
点评 本题主要考查了诱导公式,同角三角函数基本关系式的应用,考查了计算能力,属于基础题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
12.正项等比数列{an}中,a1a3+2a2a3+a1a5=16,则a2+a3的值为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
19.考取驾照是一个非常严格的过程,有的人并不能一次性通过,需要进行补考,现在有一张某驾校学员第一次考试结果汇总表:
(1)完成列联表
(2)根据列联表判断性别与考试成绩是否有关系,如果有关系求出精确地可信度,没关系请说明理由.
| 成绩 性别 | 合格 | 不合格 | 合计 |
| 男性 | 45 | 10 | |
| 女性 | 30 | ||
| 合计 | 105 |
(2)根据列联表判断性别与考试成绩是否有关系,如果有关系求出精确地可信度,没关系请说明理由.
9.设点O(0,0,0),A(2,-1,3),B(-1,4,-2),C(3,1,λ),若O,A,B,C四点共面,则实数λ等于( )
| A. | $\frac{26}{7}$ | B. | $\frac{27}{7}$ | C. | 4 | D. | $\frac{29}{7}$ |
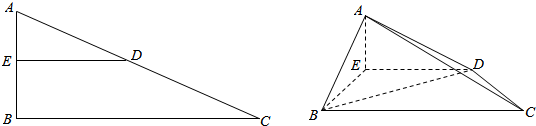
16.已知直角△ABC中,∠C=90°,∠B=30°,AB=4,D为AB的中点,沿中线将△ACD折起使得AB=$\sqrt{13}$,则二面角A-CD-B的大小为( )
| A. | 60° | B. | 90° | C. | 120° | D. | 150° |