题目内容
3.设M=a+$\frac{1}{a-2}$(2<a<3).N=x(4$\sqrt{3}$-3x)(0<x<$\frac{4\sqrt{3}}{3}$),则M,N的大小关系为( )| A. | M>N | B. | M<N | C. | M≥N | D. | M≤N |
分析 由于M=a+$\frac{1}{a-2}$=a-2+$\frac{1}{a-2}$+2(2<a<3)在(2,3)上单调递减,可得M>4,利用基本不等式可求得N的范围,从而可比较二者的大小
解答 解:∵M=a+$\frac{1}{a-2}$=a-2+$\frac{1}{a-2}$+2,
而0<a-2<1,
又∵y=x+$\frac{1}{x}$在(0,1]上单调递减,
∴M在(2,3)上单调递减,
∴M>(3-2)+$\frac{1}{3-2}$+2=4;
又0<x<$\frac{4\sqrt{3}}{3}$,
∴0<N=x(4-3x)=$\frac{1}{3}$•3x(4-3x)≤$\frac{1}{3}$[$\frac{3x+(4-3x)}{2}$]2=$\frac{4}{3}$.
∴M>N
故选:A
点评 本题考查对勾函数函数的性质及基本不等式,关键在于合理转化,利用基本不等式解决问题,考查综合运用数学知识的能力,属于中档题.

练习册系列答案
相关题目
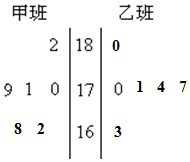 随机抽取某中学甲乙两班各6名学生,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.
随机抽取某中学甲乙两班各6名学生,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.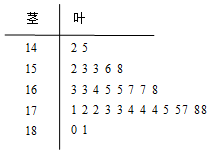 从某校的高一学生中采用系统抽样法选出30人测量其身高,数据的茎叶图如图(单位:cm):若高一年级共有600人,据上图估算身高在1.70m以上的大约有300人.
从某校的高一学生中采用系统抽样法选出30人测量其身高,数据的茎叶图如图(单位:cm):若高一年级共有600人,据上图估算身高在1.70m以上的大约有300人.