题目内容
11.对于函数y=2sin(3x+$\frac{π}{4}$),求出其定义域,值域,最小正周期,以及单调性.分析 利用正弦函数的性质,即可求得函数y=2sin(3x+$\frac{π}{4}$)的定义域、最小正周期、值域、单调性.
解答 解:函数y=2sin(3x+$\frac{π}{4}$)的定义域为R;
∵-1≤sin(3x+$\frac{π}{4}$)≤1,
∴-2≤2sin(3x+$\frac{π}{4}$)≤2,
∴函数y=2sin(3x+$\frac{π}{4}$)的值域为:[-2,2];
最小正周期T=$\frac{2π}{3}$,
由2kπ-$\frac{π}{2}$≤3x+$\frac{π}{4}$≤2kπ+$\frac{π}{2}$(k∈Z)得:$\frac{2}{3}$kπ-$\frac{π}{4}$≤x≤$\frac{2}{3}$kπ+$\frac{π}{12}$(k∈Z),
∴函数y=2sin(3x+$\frac{π}{4}$)的单调增区间为[$\frac{2}{3}$kπ-$\frac{π}{4}$,$\frac{2}{3}$kπ+$\frac{π}{12}$](k∈Z);
由2kπ+$\frac{π}{2}$≤3x+$\frac{π}{4}$≤2kπ+$\frac{3π}{2}$(k∈Z)得:$\frac{2}{3}$kπ+$\frac{π}{12}$≤x≤$\frac{2}{3}$kπ+$\frac{5π}{12}$(k∈Z),
∴函数y=2sin(3x+$\frac{π}{4}$)的单调减区间为[$\frac{2}{3}$kπ+$\frac{π}{12}$,$\frac{2}{3}$kπ+$\frac{5π}{12}$](k∈Z).
点评 本题考查正弦函数的性质,着重考查其定义域、最小正周期、值域、单调性,属于基础题.

练习册系列答案
相关题目
1.直线2x-2y+1=0的倾斜角是( )
| A. | 30° | B. | 45° | C. | 120° | D. | 135° |
2.设z=kx+y,其中实数x,y满足$\left\{\begin{array}{l}{x+y-2≥0}\\{x-2y+4≥0}\\{2x-y-4≤0}\end{array}\right.$若z的最大值为12,则实数k=( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
16.已知集合M={x||x-1|<1},N={x|x2>4},则( )
| A. | M∩N=∅ | B. | M∩N=M | C. | M∩N=N | D. | M∪N=R |
3.设M=a+$\frac{1}{a-2}$(2<a<3).N=x(4$\sqrt{3}$-3x)(0<x<$\frac{4\sqrt{3}}{3}$),则M,N的大小关系为( )
| A. | M>N | B. | M<N | C. | M≥N | D. | M≤N |
1.函数f(x)=|x2-a|在区间[-1,1]上的最大值是a,那么实数a的取值范围是( )
| A. | [0,+∞) | B. | [$\frac{1}{2}$,1] | C. | [$\frac{1}{2}$,+∞) | D. | [1,+∞) |
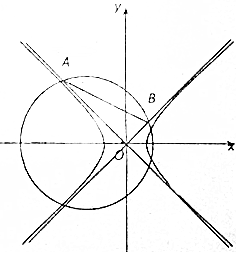 如图,双曲线k2x2-y2=1(k>0)的两条渐近线与圆(x+2)2+y2=5在x轴的上方交于A、B两点.
如图,双曲线k2x2-y2=1(k>0)的两条渐近线与圆(x+2)2+y2=5在x轴的上方交于A、B两点.