题目内容
19.写出一个以椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1和双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的离心率为根的方程x2-$\frac{5}{2}$x+1=0.分析 求出椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1和双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的离心率.利用韦达定理,可得结论.
解答 解:椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的离心率为$\frac{1}{2}$,双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的离心率为2,
∴2+$\frac{1}{2}$=$\frac{5}{2}$,2×$\frac{1}{2}$=1,
∴以椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1和双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的离心率为根的方程为x2-$\frac{5}{2}$x+1=0.
故答案为:x2-$\frac{5}{2}$x+1=0.
点评 本题以椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1和双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的离心率为载体,考查一元二次方程,考查学生的计算能力,正确求出椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1和双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的离心率是关键.

练习册系列答案
相关题目
10.直线y=k(x-3)与双曲线$\frac{x^2}{9}-\frac{y^2}{4}=1$只有一个公共点,则k的值有( )
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 无数个 |
7.已知函数f(x)=|sinx|+|cosx|,则下列结论中错误的是( )
| A. | f(x)是周期函数 | B. | f(x)的对称轴方程为x=$\frac{kπ}{4}$,k∈Z | ||
| C. | f(x)在区间($\frac{π}{4}$,$\frac{3π}{4}$)上为增函数 | D. | 方程f(x)=$\frac{6}{5}$在区间[-$\frac{3}{2}$π,0]上有6个根 |
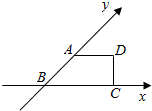 一个水平放置的平面图形的斜二测直观图是直角梯形ABCD,如图所示,∠ABC=45°,$AB=AD=\sqrt{2}$,DC⊥BC,这个平面图形的面积为$4+\sqrt{2}$.
一个水平放置的平面图形的斜二测直观图是直角梯形ABCD,如图所示,∠ABC=45°,$AB=AD=\sqrt{2}$,DC⊥BC,这个平面图形的面积为$4+\sqrt{2}$.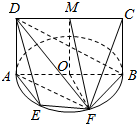 如图所示,矩形ABCD所在的平面垂直圆O所在的平面,AB是圆O的直径,M是CD上一点,且DM=EF,E、F是圆O上的点,∠EAF=∠FAB=30°.
如图所示,矩形ABCD所在的平面垂直圆O所在的平面,AB是圆O的直径,M是CD上一点,且DM=EF,E、F是圆O上的点,∠EAF=∠FAB=30°.