题目内容
17.已知函数$f(x)=\frac{1}{2}a{x^2}+3lnx,g(x)=-bx$,其中a,b∈R.设h(x)=f(x)-g(x),若$f'(\frac{{\sqrt{2}}}{2})=0$,且f′(1)=g(-1)-2.(1)求a,b的值;
(2)求函数h(x)的图象在点(1,-4)处的切线方程.
分析 (1)求出函数的导数,利用已知条件列出方程即可求出a,b的值.
(2)求出切点坐标,切线的斜率,即可求解切线方程.
解答 解:(1)因为${f^/}(x)=ax+\frac{3}{x}$,所以f′(1)=a+3.
由f′(1)=g(-1)-2可得b=a+5,又${f^'}(\frac{{\sqrt{2}}}{2})=0$,
所以${f^/}(\frac{{\sqrt{2}}}{2})=\frac{{\sqrt{2}}}{2}a+3\sqrt{2}=0$,
所以a=-6,b=-1.
(2)h(x)=-3x2+3lnx-x点(1,-4)为切点,
故${h^/}(x)=-6x+\frac{3}{x}-1$,
斜率k=h′(1)=-4,
故切线方程为y=-4x.
点评 本题考查切线方程的求法,函数的解析式的求法,导数的应用,考查计算能力.

练习册系列答案
相关题目
5.某几何体的三视图如图所示,当xy最大时,该几何体外接球的表面积为( )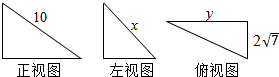

| A. | 32π | B. | 64π | C. | 128π | D. | 136π |
12.已知定义域为R的函数f(x)以4为周期,且函数f(x)=$\left\{\begin{array}{l}{\sqrt{1-{x}^{2}},x∈(-1,1]}\\{2-|x-2|,x∈(1,3]}\end{array}\right.$,若满足函数g(x)=f(x)-mx(m>0)恰有5个零点,则m的取值范围为( )
| A. | ($\frac{\sqrt{15}}{15}$,$\frac{1}{3}$) | B. | [$\frac{1}{5}$,$\frac{\sqrt{15}}{15}$) | C. | ($\frac{1}{5}$,$\frac{\sqrt{15}}{15}$] | D. | ($\frac{1}{7}$,$\frac{1}{5}$] |
2.已知椭圆的两个焦点为F1(-$\sqrt{5}$,0),F2($\sqrt{5}$,0),M是椭圆上一点,若MF1⊥MF2,|MF1||MF2|=8,则该椭圆的方程是( )
| A. | $\frac{{x}^{2}}{7}$+$\frac{{y}^{2}}{2}$=1 | B. | $\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{7}$=1 | C. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{9}$=1 |
7.已知函数f(x)=|sinx|+|cosx|,则下列结论中错误的是( )
| A. | f(x)是周期函数 | B. | f(x)的对称轴方程为x=$\frac{kπ}{4}$,k∈Z | ||
| C. | f(x)在区间($\frac{π}{4}$,$\frac{3π}{4}$)上为增函数 | D. | 方程f(x)=$\frac{6}{5}$在区间[-$\frac{3}{2}$π,0]上有6个根 |
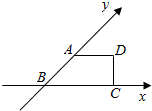 一个水平放置的平面图形的斜二测直观图是直角梯形ABCD,如图所示,∠ABC=45°,$AB=AD=\sqrt{2}$,DC⊥BC,这个平面图形的面积为$4+\sqrt{2}$.
一个水平放置的平面图形的斜二测直观图是直角梯形ABCD,如图所示,∠ABC=45°,$AB=AD=\sqrt{2}$,DC⊥BC,这个平面图形的面积为$4+\sqrt{2}$.