题目内容
已知点A(-3,0),B(3,-3),C(1,3).
(1)求过点C且和直线AB平行的直线l1的方程;
(2)若过B的直线l2和直线BC关于直线AB对称,求l2的方程.
(1)求过点C且和直线AB平行的直线l1的方程;
(2)若过B的直线l2和直线BC关于直线AB对称,求l2的方程.
考点:与直线关于点、直线对称的直线方程,直线的一般式方程与直线的平行关系
专题:直线与圆
分析:(1)求出AB的斜率,根据直线平行的斜率关系,利用点斜式方程即可求出直线l1的方程;
(2)求出C关于直线AB的对称点.利用两点是非常即可求l2的方程.
(2)求出C关于直线AB的对称点.利用两点是非常即可求l2的方程.
解答:
解:(1)直线AB的斜率为k=
=-
,
则过点C且和直线AB平行的直线l1的方程的斜率k=-
;
则直线方程为y-3=-
(x-1),即y=-
x+
;
(2)直线AB的方程为y=-
(x+3),
设C关于AB对称的点的坐标为D(a,b),
则
,即
,
即D(-3,-5),
则l2经过点B(3,-3),
则l2的方程为
=
.
即x-3y-12=0.
| -3-0 |
| 3-(-3) |
| 1 |
| 2 |
则过点C且和直线AB平行的直线l1的方程的斜率k=-
| 1 |
| 2 |

则直线方程为y-3=-
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
(2)直线AB的方程为y=-
| 1 |
| 2 |
设C关于AB对称的点的坐标为D(a,b),
则
|
|
即D(-3,-5),
则l2经过点B(3,-3),
则l2的方程为
| y+3 |
| -5+3 |
| x-3 |
| -3-3 |
即x-3y-12=0.
点评:本题主要考查直线方程的求解,根据直线平行以及点的对称性,利用点斜式方程和两点式方程是求直线方程的常用方法.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
函数f(x)=
的定义域是( )
| 1-lnx |
| A、(0.e) |
| B、(0,e] |
| C、[e,+∞) |
| D、(e,+∞) |
已知函数f(x)=
,g(x)=x2-2x,若关于x的方程f[g(x)]=k有四个不相等的实根,则实数k∈( )
|
A、(
| ||
B、(
| ||
| C、(0,1) | ||
| D、(-1,1) |
若直线y=x+b与圆x2+y2=2相切,则b的值为( )
| A、±4 | ||
B、±2
| ||
| C、±2 | ||
D、±
|
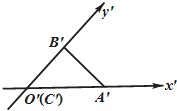 水平放置的△ABC由“斜二测画法”画得的直观图如图所示,已知A′C′=3,B′C′=2,则AB边的实际长度为( )
水平放置的△ABC由“斜二测画法”画得的直观图如图所示,已知A′C′=3,B′C′=2,则AB边的实际长度为( ) 在高中数学课本中我们见过许多的“信息技术应用”,我们可以利用几何画板软件的拖动、动画及计算等功能来研究许多数学问题.比如:在平面内做一条线段KL,以定点A为圆心,以|KL|为半径作一圆,在圆内取一定点F,在圆上取动点B,作线段BF的中垂线与圆A的半径AB交于点P,当点B在圆上运动时,就会发现点P的运动轨迹.
在高中数学课本中我们见过许多的“信息技术应用”,我们可以利用几何画板软件的拖动、动画及计算等功能来研究许多数学问题.比如:在平面内做一条线段KL,以定点A为圆心,以|KL|为半径作一圆,在圆内取一定点F,在圆上取动点B,作线段BF的中垂线与圆A的半径AB交于点P,当点B在圆上运动时,就会发现点P的运动轨迹.