题目内容
已知ξ～N（0，s2），若P（ξ＞2）=0.023，则P（-2≤ξ≤2）=（ ）
| A、0.477 |
| B、0.628 |
| C、0.954 |
| D、0.977 |
考点：正态分布曲线的特点及曲线所表示的意义
专题：计算题,概率与统计
分析：画出正态分布N（0，1）的密度函数的图象，由图象的对称性可得结果．
解答：
解：因为随机变量ξ服从正态分布N（0，s2），
所以正态曲线关于直线x=0对称，
又P（ξ＞2）=0.023，
所以P（ξ＜-2）=0.023，
所以P（-2＜ξ＜2）=1-P（ξ＞2）-P（ξ＜-2）=1-2×0.023=0.954，
故选C．
解：因为随机变量ξ服从正态分布N（0，s2），所以正态曲线关于直线x=0对称，
又P（ξ＞2）=0.023，
所以P（ξ＜-2）=0.023，
所以P（-2＜ξ＜2）=1-P（ξ＞2）-P（ξ＜-2）=1-2×0.023=0.954，
故选C．
点评：本题主要考查正态分布的概率求法，结合正态曲线，加深对正态密度函数的理解．
练习册系列答案
高效智能课时作业系列答案
相关题目
已知双曲线
+
=1的离心率e＜2，则k的取值范围是（ ）
| x2 |
| 4 |
| y2 |
| k |
| A、k＜0或k＞3 |
| B、-3＜k＜0 |
| C、-12＜k＜0 |
| D、-8＜k＜3 |
已知函数f（x）=ax+x-b的零点x1∈（n，n+1）（n∈Z），其中常数a，b满足2a=3，3b=2，则n等于（ ）
| A、-1 | B、-2 | C、1 | D、2 |
求证：
+
＞
（ ）
| 2 |
| 3 |
| 5 |
| A、综合法 |
| B、分析法 |
| C、综合法、分析法配合使用 |
| D、间接证法 |
已知过A（-2，m），B（m，4）两点的直线与直线y=
x垂直，则m的值为（ ）
| 1 |
| 2 |
| A、4 | B、-8 | C、-2 | D、-1 |
在等比数列中，an＞0，且a2a7a12=729，则2a3a11=（ ）
| A、81 | B、162 |
| C、243 | D、96 |
在直角坐标系中，方程（x+y-1）（
-y）=0所表示的曲线为（ ）
| 3+2x-x2 |
| A、一条直线和一个圆 |
| B、一条线段和一个圆 |
| C、一条直线和半个圆 |
| D、一条线段和半个圆 |
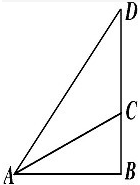已知某建筑公司在高出地面20m的小山顶建造了一座电视台CD，如图所示，设B为电视塔的正下方水平面上的点，在坡脚取一点A测得∠CAD=45°，∠CAB=α，且tanα=