题目内容
在等差数列{an}中,a1=1,a7=4,数列{bn}是等比数列,已知b2=2,b3=
,则满足bn<
的最小自然数n为 .
| 2 |
| 3 |
| 1 |
| a80 |
考点:等差数列的性质
专题:等差数列与等比数列
分析:根据题意和等差、等比数列的性质、通项公式分别求出公差和公比,再求出a80、bn代入不等式化简即可,
解答:
解:因为等差数列{an}中,a1=1,a7=4,所以公差d=
=
,
则a80=a1+79d=1+79×
=
,
因为数列{bn}是等比数列,已知b2=2,b3=
,所以公比q=
=
,
所以bn=b2•qn-2=2•(
)n-2,
代入bn<
得,2•(
)n-2<
,解得n>6,
所以满足bn<
的最小自然数n为7,
故答案为:7.
| a7-a1 |
| 7-1 |
| 1 |
| 2 |
则a80=a1+79d=1+79×
| 1 |
| 2 |
| 81 |
| 2 |
因为数列{bn}是等比数列,已知b2=2,b3=
| 2 |
| 3 |
| b3 |
| b2 |
| 1 |
| 3 |
所以bn=b2•qn-2=2•(
| 1 |
| 3 |
代入bn<
| 1 |
| a80 |
| 1 |
| 3 |
| 2 |
| 81 |
所以满足bn<
| 1 |
| a80 |
故答案为:7.
点评:本题考查了等差、等比数列的性质、通项公式,以及指数不等式,属于基础题.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
已知过A(-2,m),B(m,4)两点的直线与直线y=
x垂直,则m的值为( )
| 1 |
| 2 |
| A、4 | B、-8 | C、-2 | D、-1 |
函数y=
的定义域为M,值域为N,则M∩N=( )
| 3x-2 |
| A、M | ||
| B、(1,+∞) | ||
C、(-∞,
| ||
| D、N |
方程
-
=1表示椭圆,则a的取值范围是( )
| x2 |
| 3 |
| y2 | ||
sin(2a+
|
A、-
| ||||
B、kπ-
| ||||
C、
| ||||
D、2kπ-
|
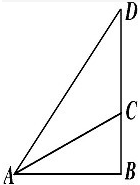 已知某建筑公司在高出地面20m的小山顶建造了一座电视台CD,如图所示,设B为电视塔的正下方水平面上的点,在坡脚取一点A测得∠CAD=45°,∠CAB=α,且tanα=
已知某建筑公司在高出地面20m的小山顶建造了一座电视台CD,如图所示,设B为电视塔的正下方水平面上的点,在坡脚取一点A测得∠CAD=45°,∠CAB=α,且tanα=