题目内容
10.若双曲线$\frac{x^2}{9}-\frac{{y{\;}^2}}{7}=1$上一点P到右焦点的距离为1,则点P到原点的距离是3.分析 利用双曲线的方程,求出实轴长,焦距的长,利用已知条件求解即可.
解答 解:双曲线$\frac{x^2}{9}-\frac{{y{\;}^2}}{7}=1$的实轴长为:6,焦距为:8,
双曲线$\frac{x^2}{9}-\frac{{y{\;}^2}}{7}=1$上一点P到右焦点的距离为1,满足c-a=1,所以P为双曲线右顶点,
可得点P到原点的距离是:3.
故答案为:3.
点评 本题考查双曲线的简单性质的应用,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.直线 y+3=0的倾斜角是( )
| A. | 0° | B. | 45° | C. | 90° | D. | 不存在 |
18.已知m,n为两条直线,α,β为两个不同的平面,则下列说法正确的是( )
| A. | 若m∥α,α∥β,则m∥β | B. | 若α⊥β,m?α,则m⊥β | ||
| C. | 若m⊥α,m∥n,α⊥β,则n∥β | D. | 若m⊥α,m∥n,α∥β,则n⊥β |
2.关于幂函数y=xk及其图象,有下列四个命题:
①其图象一定不通过第四象限;
②当k<0时,其图象关于直线y=x对称;
③当k>0时,函数y=xk是增函数;
④y=xk的图象与y=x-k的图象至少有两个交点
其中正确的命题个数是( )
①其图象一定不通过第四象限;
②当k<0时,其图象关于直线y=x对称;
③当k>0时,函数y=xk是增函数;
④y=xk的图象与y=x-k的图象至少有两个交点
其中正确的命题个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
19.向量a=(2,-2),b=(4,x)且a,b共线,则x的值为( )
| A. | 1 | B. | -1 | C. | -3 | D. | -4 |
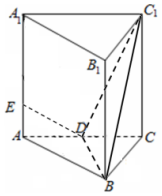 已知正三棱柱ABC-A1B1C1中,AB=AA1=2,点D为AC的中点,点E为AA1上.
已知正三棱柱ABC-A1B1C1中,AB=AA1=2,点D为AC的中点,点E为AA1上.