题目内容
已知函数f（x）=4cosxsinx（x+
）-1．求f（x）的单调增区间 ．
| π |
| 6 |
考点：三角函数中的恒等变换应用,正弦函数的图象
专题：三角函数的求值,三角函数的图像与性质
分析：首先通过三角函数的恒等变换，把三角函数变形成正弦型函数，进一步利用整体思想求出函数的单调递增区间．
解答：
解：函数f（x）=4cosxsin（x+
）-1
=4cosx（sinx
+
cosx）-1
=
sin2x+cos2x
=2sin（2x+
）
令：-
+2kπ≤2x+
≤
+2kπ（k∈Z）
解得：-
+kπ≤x≤
+kπ
所以函数f（x）的单调递增区间为：[-
+kπ，
+kπ]（k∈Z）
故答案为：[-
+kπ，
+kπ]（k∈Z）
| π |
| 6 |
=4cosx（sinx
| ||
| 2 |
| 1 |
| 2 |
=
| 3 |
=2sin（2x+
| π |
| 6 |
令：-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
解得：-
| π |
| 3 |
| π |
| 6 |
所以函数f（x）的单调递增区间为：[-
| π |
| 3 |
| π |
| 6 |
故答案为：[-
| π |
| 3 |
| π |
| 6 |
点评：本题考查的知识要点：三角函数关系式的恒等变换，正弦型函数的性质的应用，利用整体思想求正弦型函数的单调区间．属于基础题型．
练习册系列答案
相关题目
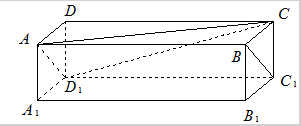
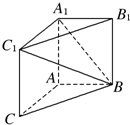如图，在三棱柱ABCA1B1C1中，AA1C1C是边长为4的正方形，平面ABC⊥平面AA1C1C，AB=3，BC=5．
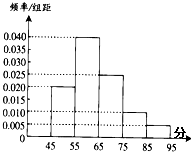为了调查某班学生做数学题的基本能力，随机抽查了部分学生某次做一份满分为100分的数学试题，他们所得分数的分组区间为[45，55），[55，65），[65，75），[75，85），[85，95），由此得到频率分布直方图如图，则这些学生的平均分为