题目内容
函数f(x)在[a,b]上有定义,若对任意x1,x2∈[a,b],有f(
)≤
[f(x1)+f(x2)],则称f(x)在[a,b]上具有性质P.设,现给出如下命题:
(1)f(x)=
在[1,3]上具有性质P;
(2)若f(x)在[1,3]上具有性质P,f(x)在x=2处取得最大值1,则f(x)=1,x∈[1,3];
(3)若f(x)在[1,3]上具有性质P,则f(x)在[1,3]上的图象是连续不断的;
(4)若f(x)在[1,3]上具有性质P,f(x2)在[1,
]上具有性质P;
其中正确的命题是 .
| x1+x2 |
| 2 |
| 1 |
| 2 |
(1)f(x)=
| 1 |
| x |
(2)若f(x)在[1,3]上具有性质P,f(x)在x=2处取得最大值1,则f(x)=1,x∈[1,3];
(3)若f(x)在[1,3]上具有性质P,则f(x)在[1,3]上的图象是连续不断的;
(4)若f(x)在[1,3]上具有性质P,f(x2)在[1,
| 3 |
其中正确的命题是
考点:抽象函数及其应用
专题:函数的性质及应用
分析:根据f(x)在[a,b]上具有性质P的定义,结合函数凸凹性的性质,利用数形结合即可得到结论.
解答:
解:(1)f(x)=
在[1,3]上为减函数,则由图象可知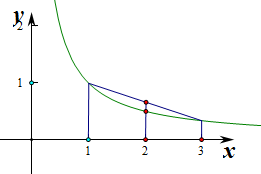 对任意x1,x2∈[1,3],有f(
对任意x1,x2∈[1,3],有f(
)≤
[f(x1)+f(x2)],成立,故(1)正确,
(2)在[1,3]上,f(2)=f[
]≤
[f(x)+f(4-x)],
∵F(x)在x=2时取得最大值1,
∴
,
∴f(x)=1,即对任意的x∈[1,3],有f(x)=1,故(2)正确;
(3)反例:f(x)=
,在[1,3]上满足性质P,
但f(x)在[1,3]上不是连续函数,故(3)不成立;
(4)反例:f(x)=-x在[1,3]上满足性质P,但f(x2)=-x2在[1,
]上不满足性质P,故(4)不成立;
综上正确的命题是(1),(2)
| 1 |
| x |
 对任意x1,x2∈[1,3],有f(
对任意x1,x2∈[1,3],有f(| x1+x2 |
| 2 |
| 1 |
| 2 |
(2)在[1,3]上,f(2)=f[
| x+(4-x) |
| 2 |
| 1 |
| 2 |
∵F(x)在x=2时取得最大值1,
∴
|
∴f(x)=1,即对任意的x∈[1,3],有f(x)=1,故(2)正确;
(3)反例:f(x)=
|
但f(x)在[1,3]上不是连续函数,故(3)不成立;
(4)反例:f(x)=-x在[1,3]上满足性质P,但f(x2)=-x2在[1,
| 3 |
综上正确的命题是(1),(2)
点评:本题是一道新定义题,实质上是考查函数的凹凸性及应用,解题的关键是理解这一性质,灵活运用这一性质,可通过举反例,以及利用数形结合是解决本题的关键.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
若函数f(x)=|x+1|+|2x-a|的最小值为3,则实数a的值为( )
| A、4或-8 | B、-5或-8 |
| C、1或-5 | D、1或4 |
设点P在曲线y=x2上,点Q在直线y=2x-2上,则PQ的最小值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
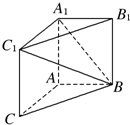 如图,在三棱柱ABCA1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
如图,在三棱柱ABCA1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5. 如图,△ABC是边长为2
如图,△ABC是边长为2