题目内容
在数列{an}中,已知a1=1,a2=3,其前n项和Sn满足Sn=
(a1+an)(n∈N+).
(1)求a3,a4,a5的值;
(2)求an的表达式;
(3)对于任意的正整数n≥2,求证:a1a2…an>(2n+1)
.
| n |
| 2 |
(1)求a3,a4,a5的值;
(2)求an的表达式;
(3)对于任意的正整数n≥2,求证:a1a2…an>(2n+1)
| n-1 |
| 2 |
考点:数学归纳法,数列的求和
专题:等差数列与等比数列
分析:(1)依次令n=3,4,5可求得a3,a4,a5的值.
(2)由 (1)猜想an=2n-1,然后利用数学归纳法证明.
(3)由{an}为等差数列,得a1+an+1=a2+an=…=an+a2=an+1+a1.由xy=
-
,知x+y一定时,要使xy最小,则|x-y|最大.由此能证明a1a2…an>(2n+1)
.
(2)由 (1)猜想an=2n-1,然后利用数学归纳法证明.
(3)由{an}为等差数列,得a1+an+1=a2+an=…=an+a2=an+1+a1.由xy=
| (x+y)2 |
| 4 |
| (x-y)2 |
| 4 |
| n-1 |
| 2 |
解答:
(1)解:∵a1=1,a2=3,其前n项和Sn满足Sn=
(a1+an)(n∈N+).
∴n=3时,4+a3=
(1+a3),解得a3=5;
n=4时,9+a4=
(1+a4),解得a4=7;
n=5时,16+a5=
(1+a5),解得a5=9.
(2)解:由 (1)猜想an=2n-1,
下面用数学归纳法证明:
①当n=1,2时结论显然成立.
②假设n=k(k∈N,k≥2)时结论成立,即ak=2k-1,
则ak+1=Sk+1-Sk=
(1+ak+1)-
(1+ak)=
+
ak+1-
⇒(k-1)ak+1=2k2-k-1⇒ak+1=2k+1,
故当n=k+1时结论成立.
综上知结论成立.
(3)证明:由 (2)知{an}为等差数列,
故a1+an+1=a2+an=…=an+a2=an+1+a1.
由xy=
-
,知x+y一定时,要使xy最小,则|x-y|最大.
∵|a1-an+1|>|ak-an+2-k|(2≤k≤n),
∴(a1a2…an+1)2=(a1an+1)(a2an)…(an+1a1)>(a1an+1)n+1,
∴a1a2…an+1>(a1an+1)
=(2n+1)
,
从而a1a2…an>(2n+1)
.
| n |
| 2 |
∴n=3时,4+a3=
| 3 |
| 2 |
n=4时,9+a4=
| 4 |
| 2 |
n=5时,16+a5=
| 5 |
| 2 |
(2)解:由 (1)猜想an=2n-1,
下面用数学归纳法证明:
①当n=1,2时结论显然成立.
②假设n=k(k∈N,k≥2)时结论成立,即ak=2k-1,
则ak+1=Sk+1-Sk=
| k+1 |
| 2 |
| k |
| 2 |
| 1 |
| 2 |
| k+1 |
| 2 |
| k(2k-1) |
| 2 |
故当n=k+1时结论成立.
综上知结论成立.
(3)证明:由 (2)知{an}为等差数列,
故a1+an+1=a2+an=…=an+a2=an+1+a1.
由xy=
| (x+y)2 |
| 4 |
| (x-y)2 |
| 4 |
∵|a1-an+1|>|ak-an+2-k|(2≤k≤n),
∴(a1a2…an+1)2=(a1an+1)(a2an)…(an+1a1)>(a1an+1)n+1,
∴a1a2…an+1>(a1an+1)
| n+1 |
| 2 |
| n+1 |
| 2 |
从而a1a2…an>(2n+1)
| n-1 |
| 2 |
点评:本题考查数列的通项公式的求法,考查不等式的证明,解题时要认真审题,注意数学归纳法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在长方体ABCD-A1B1C1D1中,AB=2,BC=2,DD1=3,则AC与BD1所成角的余弦值为( )
| A、0 | ||||
B、
| ||||
C、-
| ||||
D、
|
 如图,已知长方形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起到△APM,使得平面APM⊥平面ABCM,点E在线段PB上,且PE=
如图,已知长方形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起到△APM,使得平面APM⊥平面ABCM,点E在线段PB上,且PE=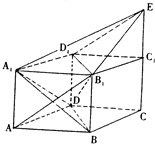 如图,已知直四棱柱ABCD-A1B1C1D1中,AB=AA1,底面ABCD为菱形,∠ADC=120°,E为CC1延长线上一点.
如图,已知直四棱柱ABCD-A1B1C1D1中,AB=AA1,底面ABCD为菱形,∠ADC=120°,E为CC1延长线上一点.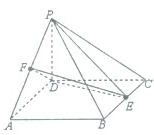 如图,四棱锥P-ABCD的底面ABCD为菱形,PD⊥平面ABCD,PD=AB=2,∠BAD=60°,E、F分别为BC、PA的中点.
如图,四棱锥P-ABCD的底面ABCD为菱形,PD⊥平面ABCD,PD=AB=2,∠BAD=60°,E、F分别为BC、PA的中点.