题目内容
设函数f(x)=|x-
|+|x-a|,x∈R.
(Ⅰ)求证:当a=-
时,不等式lnf(x)>1成立.
(Ⅱ)关于x的不等式f(x)≥a在R上恒成立,求实数a的最大值.
| 5 |
| 2 |
(Ⅰ)求证:当a=-
| 1 |
| 2 |
(Ⅱ)关于x的不等式f(x)≥a在R上恒成立,求实数a的最大值.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(Ⅰ)当a=-
时,根据f(x)=
的最小值为3,可得lnf(x)最小值为ln3>lne=1,不等式得证.
(Ⅱ)由绝对值三角不等式可得 f(x)≥|a-
|,可得|a-
|≥a,由此解得a的范围.
| 1 |
| 2 |
|
(Ⅱ)由绝对值三角不等式可得 f(x)≥|a-
| 5 |
| 2 |
| 5 |
| 2 |
解答:
解:(Ⅰ)证明:∵当a=-
时,f(x)=|x-
|+|x+
|=
的最小值为3,
∴lnf(x)最小值为ln3>lne=1,∴lnf(x)>1成立.
(Ⅱ)由绝对值三角不等式可得 f(x)=|x-
|+|x-a|≥|(x-
)-(x-a)|=|a-
|,
再由不等式f(x)≥a在R上恒成立,可得|a-
|≥a,
∴a-
≥a,或 a-
≤-a,解得a≤
,故a的最大值为
.
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
|
∴lnf(x)最小值为ln3>lne=1,∴lnf(x)>1成立.
(Ⅱ)由绝对值三角不等式可得 f(x)=|x-
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
再由不等式f(x)≥a在R上恒成立,可得|a-
| 5 |
| 2 |
∴a-
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 4 |
| 5 |
| 4 |
点评:本题主要考查绝对值不等式的解法,体现了等价转化和分类讨论的数学思想,函数的恒成立问题,属于基础题.

练习册系列答案
相关题目
复数
+4+i的共轭复数是( )
| 5(2+i) |
| i-2 |
| A、1-3i | ||
| B、1+3i | ||
C、-1-
| ||
D、-1+
|
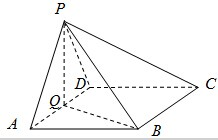 如图四棱锥P-ABCD的底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
如图四棱锥P-ABCD的底面ABCD为菱形,∠BAD=60°,Q为AD的中点.