题目内容

6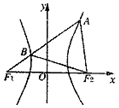．如图，F1、F2是双曲线$\frac{x^2}{9}-\frac{y^2}{b^2}=1（b＞0）$的左、右焦点，过F1的直线l与双曲线分别交于点A、B，若△ABF2为等边三角形，则△BF1F2的面积为（　　）
A．$8\sqrt{3}$B．$9\sqrt{3}$C．$18\sqrt{3}$D．$27\sqrt{3}$

分析 由双曲线的定义，可得|BF1|=2a，|BF2|=|BF1|+2a=4a，即可求出△BF1F2的面积．

解答 解：根据双曲线的定义，可得|AF1|-|AF2|=2a，
∵△ABF2是等边三角形，即|AF2|=|AB|
∴|AF1|-|AB|=|BF1|=2a
又∵|BF2|-|BF1|=2a，
∴|BF2|=|BF1|+2a=4a，
在双曲线中：a2=9，
∴△BF1F2的面积为$\frac{1}{2}•2a•4a•\frac{\sqrt{3}}{2}$=18$\sqrt{3}$．
故选：C．

点评 本题给出经过双曲线左焦点的直线被双曲线截得弦AB与右焦点构成等边三角形，求三角形的面积，着重考查了双曲线的定义和简单几何性质等知识，属于中档题．

练习册系列答案
相关题目
16．在平行四边形ABCD中，E，F分别是CD和BC的中点，若$\overrightarrow{AE}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$（x，y∈R），则2x+y=2；若$\overrightarrow{AC}$=λ$\overrightarrow{AE}$+μ$\overrightarrow{AF}$（λ，μ∈R），则3λ+3μ=4．
17．已知数列{an}满足：a1=2，an+1=$\left\{\begin{array}{l}{\frac{1}{2}{a}_{n}，n为偶数}\\{{a}_{n}+1，n为奇数}\end{array}\right.$，若bn=a2n-1-1．
（Ⅰ）求证：数列{bn}是等比数列；
（Ⅱ）若数列{an}的前n项和为Sn，求S2n．
14．已知x与y之间的一组数据：
x34557
y24568
则y与x的线性回归方程为y=bx+a必过（　　）
A．（5，5）B．（4.5，5）C．（4.8，5）D．（5，6）
1．已知向量$\overrightarrow{a}$=（sinx，2cosx），$\overrightarrow{b}$=（5$\sqrt{3}$cosx，cosx），函数f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$+|$\overrightarrow{a}$|2-$\frac{7}{2}$．
（1）求函数f（x）的最小正周期；
（2）若x∈（$\frac{2π}{3}$，$\frac{11π}{12}$）时，f（x）=-3，求cos2x的值；
（3）若cosx≥$\frac{1}{2}$，x∈（-$\frac{π}{2}$，$\frac{π}{2}$），且f（x）=m有且仅有一个实根，求实数m的取值范围．
11．在直角坐标系xOy中，曲线C1的参数方程为$\left\{\begin{array}{l}x=2+\sqrt{7}cosα\\ y=\sqrt{7}sinα\end{array}\right.$（其中α为参数），曲线${C_2}：{（{x-1}）^2}+{y^2}=1$，以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系．
（Ⅰ）求曲线C1的普通方程和曲线C2的极坐标方程；
（Ⅱ）若射线$θ=\frac{π}{3}（{ρ＞0}）$与曲线C1，C2分别交于A，B两点，求|AB|．
18．已知函数f（x）=lg$\frac{1+ax}{1-x}$（a＞0）为奇函数，函数g（x）=$\frac{2}{{x}^{2}}$+b（b∈R）．
（Ⅰ）求a；
（Ⅱ）若b＞1，讨论方徎g（x）=ln|x|实数根的个数；
（Ⅲ）当x∈[$\frac{1}{3}$，$\frac{1}{2}$]时，关于x的不等式f（1-x）≤lgg（x）有解，求b的取值范围．
15．过点A（1，2）且平行于直线3x+2y-1=0的直线方程为（　　）
A．2x-3y+4=0B．3x-2y+1=0C．2x+3y-8=0D．3x+2y-7=0
16．已知函数f（x）=2x-b（2≤x≤4，b为常数）的图象经过点（3，1），则f（x）的值域为（　　）
A．[4，16]B．[2，10]C．[$\frac{1}{2}$，2]D．[$\frac{1}{2}$，+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网