题目内容
14．已知圆M与直线3x-4y=0及3x-4y+10=0都相切，圆心在直线y=-x-4上，则圆M的方程为（ ）| A． | （x+3）2+（y-1）2=1 | B． | （x-3）2+（y+1）2=1 | C． | （x+3）2+（y+1）2=1 | D． | （x-3）2+（y-1）2=1 |
分析 求出圆心坐标与半径，即可得出结论．
解答 解：到两直线3x-4y+10=0的距离都相等的直线方程为3x-4y+5=0，联立方程组$\left\{{\begin{array}{l}{3x-4y+5=0}\\{y=-x-4}\end{array}}\right.$，解得$\left\{{\begin{array}{l}{x=-3}\\{y=-1}\end{array}}\right.$．又两平行线之间的距离为2，所以，半径为1，从而圆M的方程为（x+3）2+（y+1）2=1．
故选C．
点评 本题考查圆的方程，考查学生的计算能力，确定圆心坐标与半径是关键．
练习册系列答案
阅读快车系列答案
相关题目
4．若函数f（x）=ex（sinx+acosx）在（$\frac{π}{4}$，$\frac{π}{2}$）上单调递增，则实数a的取值范围是（ ）
| A． | （-∞，1] | B． | （-∞，1） | C． | [1，+∞） | D． | （1，+∞） |
5．
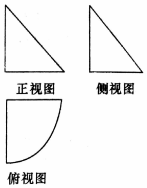一个几何体的三视图如图所示，其中正视图和侧视图是腰长为2的等腰直角三角形，俯视图是圆心角为$\frac{π}{2}$的扇形，则该几何体的表面积为（ ）
一个几何体的三视图如图所示，其中正视图和侧视图是腰长为2的等腰直角三角形，俯视图是圆心角为$\frac{π}{2}$的扇形，则该几何体的表面积为（ ）| A． | 2 | B． | π+4 | C． | $\sqrt{2}π+4$ | D． | $（{\sqrt{2}+1}）π+4$ |
2．在区间[0，1]上随机取两个数，则这两个数之和小于$\frac{3}{2}$的概率是（ ）
| A． | $\frac{1}{8}$ | B． | $\frac{3}{8}$ | C． | $\frac{5}{8}$ | D． | $\frac{7}{8}$ |
如图，在多面体ABCDEF中，底面ABCD是边长为2的菱形，∠BAD=60°，四边形BDEF是矩形，平面BDEF⊥平面ABCD
4．已知正三棱柱ABC-A1B1C1的顶点A1，B1，C1在同一球面上，且平面ABC经过球心，若此球的表面积为4π，则该三棱柱的侧面积的最大值为（ ）
| A． | $\frac{\sqrt{3}}{2}$ | B． | $\sqrt{3}$ | C． | $\frac{3\sqrt{3}}{2}$ | D． | 3$\sqrt{3}$ |