题目内容
4.设集合A={x|-1<x<1},B={x|log2x<-1},则A∩B=( )| A. | $({0,\frac{1}{2}})$ | B. | $({\frac{1}{2},1})$ | C. | (0,1) | D. | $({-1,\frac{1}{2}})$ |
分析 运用对数函数单调性,求得集合B,再由交集定义,即可得到所求.
解答 解:集合A={x|-1<x<1},
B={x|log2x<-1}={x|0<x<$\frac{1}{2}$},
则A∩B={x|0<x<$\frac{1}{2}$},
故选:A.
点评 本题考查集合的运算,主要是交集运算,同时考查对数函数单调性,属于基础题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
2.已知在△ABC中,a,b,c分别是∠BAC,∠ABC,∠ACB的对边,若过点C作垂直于AB的垂线CD,且CD=h,则下列给出的关于a,b,c,h的不等式中正确的是( )
| A. | a+b≥$\sqrt{2{h}^{2}+2{c}^{2}}$ | B. | a+b≥$\sqrt{4{h}^{2}+{c}^{2}}$ | C. | a+b≥$\sqrt{4{h}^{2}+2{c}^{2}}$ | D. | a+b≥$\sqrt{{h}^{2}+2{c}^{2}}$ |
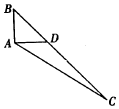 如图,在△ABC中,AD⊥AB,$\overrightarrow{BC}$=3$\overrightarrow{BD}$,|$\overrightarrow{AD}$|=1,则$\overrightarrow{AC}$•$\overrightarrow{AD}$的值为( )
如图,在△ABC中,AD⊥AB,$\overrightarrow{BC}$=3$\overrightarrow{BD}$,|$\overrightarrow{AD}$|=1,则$\overrightarrow{AC}$•$\overrightarrow{AD}$的值为( )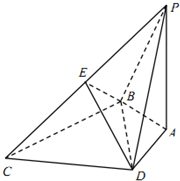 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,BC⊥PB,PC与平面ABCD所成角的正切值为$\frac{{\sqrt{2}}}{2}$,△BCD为等边三角形,PA=2$\sqrt{2}$,AB=AD,E为PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,BC⊥PB,PC与平面ABCD所成角的正切值为$\frac{{\sqrt{2}}}{2}$,△BCD为等边三角形,PA=2$\sqrt{2}$,AB=AD,E为PC的中点.