题目内容
6.定义在R上的偶函数f(x)在(-∞,0]上递减,f(-1)=0,则满足f(log2x)>0的x的取值范围是$(0,\frac{1}{2})∪(2,+∞)$.分析 根据函数奇偶性和单调性的关系,将不等式进行转化,结合绝对值不等式以及对数不等式的解法进行求解即可.
解答 解:∵偶函数f(x)在(-∞,0]上递减,f(-1)=0,
∴函数f(x)在(0,+∞]上递增,f(1)=0,
则f(log2x)>0等价为f(|log2x|)>f(1),
即|log2x|>1,
即log2x>1或log2x<-1,
得x>2或0<x<$\frac{1}{2}$,
故答案为:$(0,\frac{1}{2})∪(2,+∞)$
点评 本题主要考查不等式的求解,根据函数奇偶性和单调性的关系将不等式进行转化是解决本题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
11.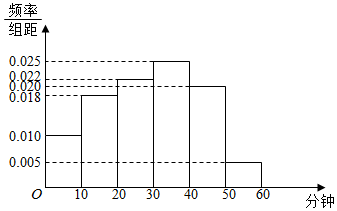 某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集到的数据分成[0,10),[10,20),[20,30),[30,40),[40,50),[50,60)六组,并作出频率分布直方图(如图).将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集到的数据分成[0,10),[10,20),[20,30),[30,40),[40,50),[50,60)六组,并作出频率分布直方图(如图).将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
(1)请根据直方图中的数据填写下面的2×2列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?
(2)现从课外体育达标学生中按分层抽样抽取5人,再从这5名学生中随机抽取2人参加体育知识问卷调查,求抽取的这2人课外锻炼时间都在[40,50)内的概率.
附参考公式与数据:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
 某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集到的数据分成[0,10),[10,20),[20,30),[30,40),[40,50),[50,60)六组,并作出频率分布直方图(如图).将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.
某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集到的数据分成[0,10),[10,20),[20,30),[30,40),[40,50),[50,60)六组,并作出频率分布直方图(如图).将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.(1)请根据直方图中的数据填写下面的2×2列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?
| 课外体育不达标 | 课外体育达标 | 合计 | |
| 男 | 60 | 30 | 90 |
| 女 | 90 | 20 | 110 |
| 合计 | 150 | 50 | 200 |
附参考公式与数据:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
12.若a>b>1,0<c<1,则( )
| A. | ac<bc | B. | abc<bac | C. | alogbc<blogac | D. | logac<logbc |
9.若x,y满足$\left\{\begin{array}{l}{2x-y≤0}\\{x+y≤3}\\{x≥0}\end{array}\right.$,则2x+y的最大值为( )
| A. | 0 | B. | 3 | C. | 4 | D. | 5 |
11.集合A={x∈N|x2-2x-3<0},B={1,x2},若A∪B={0,1,2},则这样的实数x的个数为( )
| A. | 1个 | B. | 2个 | C. | 4个 | D. | 3个 |
16.某保险的基本保费为a(单位:元),继续购买该保险的投保人成为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
设该险种一续保人一年内出险次数与相应概率如下:
(Ⅰ)求一续保人本年度的保费高于基本保费的概率;
(Ⅱ)若一续保人本年度的保费高于基本保费,求其保费比基本保费高出60%的概率;
(Ⅲ)求续保人本年度的平均保费与基本保费的比值.
| 上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
| 保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
| 一年内出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
| 概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0.05 |
(Ⅱ)若一续保人本年度的保费高于基本保费,求其保费比基本保费高出60%的概率;
(Ⅲ)求续保人本年度的平均保费与基本保费的比值.