题目内容
10.已知xy=2x+y+2(x>1),则x+y的最小值为7.分析 由题意可得y=$\frac{2x+2}{x-1}$,整体代入变形可得x+y=x-1+$\frac{4}{x-1}$+3,由基本不等式可得.
解答 解:∵xy=2x+y+2,∴y=$\frac{2x+2}{x-1}$,
∴x+y=x+$\frac{2x+2}{x-1}$=x-1+$\frac{2(x-1)+4}{x-1}$+1
=x-1+$\frac{4}{x-1}$+3≥2$\sqrt{(x-1)•\frac{4}{x-1}}$+3=7
当且仅当x-1=$\frac{4}{x-1}$即x=3时取等号,
故答案为:7.
点评 本题考查基本不等式求最值,消元并整体凑出可用基本不等式的形式是解决问题的关键,属基础题.

练习册系列答案
相关题目
20.若关于x,y的不等式组$\left\{\begin{array}{l}{x≤0}\\{x+y≥0}\\{kx-y+1≥0}\end{array}\right.$,表示的平面区域是等腰直角三角形区域,则其表示的区域面积为( )
| A. | $\frac{1}{2}$或$\frac{1}{4}$ | B. | $\frac{1}{2}$或$\frac{1}{8}$ | C. | 1或$\frac{1}{2}$ | D. | 1或$\frac{1}{4}$ |
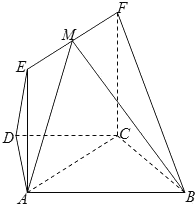 如图,平面ACFE⊥平面ABCD,四边形ACFE为矩形,在梯形ABCD中,AB∥CD,∠ABC=60°,且AD=DC=CB=AE=1,M是线段EF的中点.
如图,平面ACFE⊥平面ABCD,四边形ACFE为矩形,在梯形ABCD中,AB∥CD,∠ABC=60°,且AD=DC=CB=AE=1,M是线段EF的中点.