题目内容
球的半径为2，它的内接圆柱的底面半径为1，则圆柱的侧面积为（ ）
A、2
| ||
B、4
| ||
| C、12π | ||
| D、24π |
考点：球内接多面体,棱柱、棱锥、棱台的体积
专题：计算题,空间位置关系与距离
分析：求出内接圆柱的高，再求圆柱的侧面积．
解答：
解：∵球的半径为2，它的内接圆柱的底面半径为1，
∴内接圆柱的高为2
=2
，
∴圆柱的侧面积为2π×1×2
=4
π．
故选：B．
∴内接圆柱的高为2
| 4-1 |
| 3 |
∴圆柱的侧面积为2π×1×2
| 3 |
| 3 |
故选：B．
点评：本题考查圆柱的侧面积，考查学生的计算能力，比较基础．
练习册系列答案
名校课堂系列答案
相关题目
将二进制数1101化为十进制数为（ ）
| A、10 | B、11 | C、12 | D、13 |
已知a，b是两条直线，α，β是两个平面，则下列说法中正确的是（ ）
| A、若a∥b，b∥α，则a∥α |
| B、若a⊥b，b⊥α，则a⊥α |
| C、若α∥β，a?α，则a∥β |
| D、若α⊥β，a?α，则a⊥β |
已知符号函数sgnx=
，则不等式（x2-2）•sgnx＞1的解集是（ ）
|
A、(-1，1)∪(
| ||||
B、(-1，0)∪(
| ||||
C、(-∞，
| ||||
D、(-∞，-
|
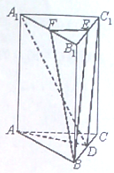如图，在三棱柱ABC-A1B1C1中，底面为正三角形，AA1⊥平面ABC，D，E，F分别为BC，B1C1，A1B1的中点．