题目内容
12.已知45°<α<90°,函数f(x)=ax+b的图象如图,则函数g(x)=loga(x+b)的图象可能为( )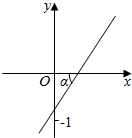
| A. | 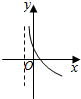 | B. | 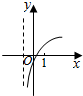 | C. | 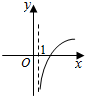 | D. |  |
分析 由题意和直线可得系数a和b的范围,结合函数图象变换可得.
解答 解:由图象令x=0可得f(x)=b∈(-1,0),∴-b∈(0,1),
∵45°<α<90°,∴直线f(x)=ax+b的斜率a=tanα>tan45°=1,
∴函数g(x)=loga(x+b)单调递增,
且是由y=logax的图象向右平移-b个单位长度得到的.
故选:C.
点评 本题考查对数函数的图象和性质,涉及直线的方程和图象,属基础题.

练习册系列答案
相关题目
7.若存在a∈R,使关于x的不等式x|x-a|<m+1在(0,1]上恒成立,则实数m的取值范围为( )
| A. | (2-2$\sqrt{2}$,2+2$\sqrt{2}$) | B. | (-1,+∞) | C. | (2-2$\sqrt{2}$,+∞) | D. | (-1,2+2$\sqrt{2}$) |
17.已知△ABC的内角A,B,C的对边分别为a,b,c,其面积为$\sqrt{3}$,且a=2,B=60°,则c等于( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
4.已知直线l经过点P(0,0),Q(-1,$\sqrt{3}$),则直线l的倾斜角为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
2.在△ABC中,设$\overrightarrow{BC}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,且|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=$\sqrt{3}$,$\overrightarrow{a}•\overrightarrow{b}$=$-\sqrt{3}$,则AB的长为( )
| A. | $\sqrt{7+2\sqrt{3}}$ | B. | $\sqrt{7-2\sqrt{3}}$ | C. | $\sqrt{7-\sqrt{3}}$ | D. | 7-2$\sqrt{3}$ |