题目内容
2.设p:?x0∈R,mx02+1≤0,q:x∈R,x2+mx+1>0,若p∨q为真命题,则实数m的取值范围是( )| A. | (-∞,2) | B. | (2,+∞) | C. | (-2,2) | D. | (-∞,2]∪[2,+∞) |
分析 先求出命题p,q为真时,实数m的取值范围,进而根据p∨q为真命题,得到答案.
解答 解:若命题p:?x0∈R,mx02+1≤0为真命题,
则m<0,
若命题q:x∈R,x2+mx+1>0,
则-2<m<2,
若p∨q为真命题,则m<0,或-2<m<2,
即m∈(-∞,2),
故选:A
点评 本题以命题的真假判断与应用为载体,考查了复合命题,全称命题和特称命题等知识点,难度中档.

练习册系列答案
相关题目
12.定义在(0,+∞)上的单调递减函数f(x),若f(x)的导函数存在且满足$\frac{f(x)}{f'(x)}>-x$,则下列不等式成立的是( )
| A. | 3f(2)<2f(3) | B. | 3f(4)<4f(3) | C. | $\frac{f(3)}{4}>\frac{f(4)}{3}$ | D. | f(2)<2f(1) |
13.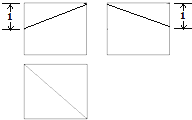 一个棱长为2的正方体被一个平面截去一部分后,剩余几何体的三视图如图所示,则此几何体的体积为( )
一个棱长为2的正方体被一个平面截去一部分后,剩余几何体的三视图如图所示,则此几何体的体积为( )
 一个棱长为2的正方体被一个平面截去一部分后,剩余几何体的三视图如图所示,则此几何体的体积为( )
一个棱长为2的正方体被一个平面截去一部分后,剩余几何体的三视图如图所示,则此几何体的体积为( )| A. | $\frac{22}{3}$ | B. | $\frac{20}{3}$ | C. | 6 | D. | 4 |
10.在数列{an}中,a1=-$\frac{1}{4}$,an=1-$\frac{1}{{a}_{n-1}}$(n>1),则a2016的值为( )
| A. | -$\frac{1}{4}$ | B. | 5 | C. | $\frac{4}{5}$ | D. | 以上都不对 |
7.根据表格中的数据用最小二乘法计算出变量x、y的线性回归方程为$\stackrel{∧}{y}$=3x-$\frac{3}{2}$,则表格中m的值是( )
| x | 0 | 1 | 2 | 3 |
| y | -1 | 1 | 8 | m |
| A. | 4 | B. | $\frac{9}{2}$ | C. | 5 | D. | 6 |
14.已知实数x,y满足不等式组$\left\{\begin{array}{l}x≥0\\ y≥0\\ x+2y≤6\\ 3x+y≤12\end{array}\right.$,且x,y∈Z,则z=2x+y的最大值是( )
| A. | 7 | B. | 8 | C. | $\frac{42}{5}$ | D. | 9 |
11.若a,b∈N,则$\frac{1}{a}$+$\frac{1}{b}$>1成立的充要条件是( )
| A. | a,b都不大于2 | B. | a,b中至少有一个等于1 | ||
| C. | a,b都大于2 | D. | a,b中至多有一个等于1 |
12.若M∪{1}={1,2,3},则M集合可以是( )
| A. | {1,2,3} | B. | {1,3} | C. | {1,2} | D. | {1} |