题目内容
12.定义在(0,+∞)上的单调递减函数f(x),若f(x)的导函数存在且满足$\frac{f(x)}{f'(x)}>-x$,则下列不等式成立的是( )| A. | 3f(2)<2f(3) | B. | 3f(4)<4f(3) | C. | $\frac{f(3)}{4}>\frac{f(4)}{3}$ | D. | f(2)<2f(1) |
分析 由题意构造g(x)=xf(x),求出g′(x),化简已知的式子后,结合题意判断出g′(x)的符号,可得g(x)在(0,+∞)上的单调性,由函数的单调性可得答案
解答 解:设g(x)=xf(x),则g′(x)=f(x)+xf′(x),
因为定义在(0,+∞)上的单调递减函数f(x),
所以x∈(0,+∞)时,f′(x)<0,
由$\frac{f(x)}{f'(x)}>-x$,得 $\frac{f(x)}{f′(x)}$+x>0,则 $\frac{xf′(x)+f(x)}{f′(x)}$>0,
则当∈(0,+∞)时,f(x)+xf′(x)<0,即g′(x)<0,
所以函数g(x)在(0,+∞)上递减,
则g(3)>g(4),即$\frac{f(3)}{4}$>$\frac{f(4)}{3}$,
故选:C.
点评 本题考查函数的单调性与导数的关系,以及构造函数法,属于中档题.

练习册系列答案
相关题目
3.把正奇数从小到大按以下方式分钟:(1),(3,5),(7,9,11),(13,15,17,19),…,其中第n组有n个正奇数,若第m组第k个正奇数是 2015,则m+k=( )
| A. | 63 | B. | 64 | C. | 65 | D. | 66 |
2.设p:?x0∈R,mx02+1≤0,q:x∈R,x2+mx+1>0,若p∨q为真命题,则实数m的取值范围是( )
| A. | (-∞,2) | B. | (2,+∞) | C. | (-2,2) | D. | (-∞,2]∪[2,+∞) |
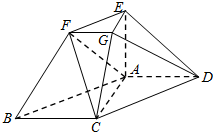 在如图所示的几何体中,四边形ABCD为平行四边形,∠ACB=90°,EA⊥平面ABCD,EF∥AB,FG∥BC,EG∥AC,AB=2EF.
在如图所示的几何体中,四边形ABCD为平行四边形,∠ACB=90°,EA⊥平面ABCD,EF∥AB,FG∥BC,EG∥AC,AB=2EF.