题目内容
10．在数列{an}中，a1=-$\frac{1}{4}$，an=1-$\frac{1}{{a}_{n-1}}$（n＞1），则a2016的值为（ ）| A． | -$\frac{1}{4}$ | B． | 5 | C． | $\frac{4}{5}$ | D． | 以上都不对 |
分析 由a1=-$\frac{1}{4}$，an=1-$\frac{1}{{a}_{n-1}}$（n＞1），可得an=an+3，利用周期性即可得出．
解答 解：数列{an}中，a1=-$\frac{1}{4}$，an=1-$\frac{1}{{a}_{n-1}}$（n＞1），
得a2=1-$\frac{1}{{a}_{1}}$=5，a3=1-$\frac{1}{{a}_{2}}$=1-$\frac{1}{5}$=$\frac{4}{5}$，a4=1-$\frac{1}{\frac{4}{5}}$=$-\frac{1}{4}$，…
∴an=an+3，
则a2016=a3×671+3=a3=$\frac{4}{5}$．
故选：C．
点评 本题考查了数列的递推关系、周期性，考查了推理能力与计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
5．
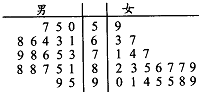某大学为了在2016年全国大学生成语听写大赛取得优秀成绩，抽调男女各20名学生组成集训队进行成语听写集训，集训结束时，为了检验集训效果，对所有集训队员进行成语听写考核，试题为听写100个常用成语（每个1分，满分100分），考核成绩如图茎叶图所示：
（I）若大于或等于80分为优秀队员，80分以下为非优秀队员，根据茎叶图填写下面2×2列联表，并判断能否有95%的把握认为队员的优秀与性别有关？
（Ⅱ）若从考核成绩95分以上（包括95分）的队员中任选两人代表这所大学参加全国大学生成语听写大赛，求至少有一名男队员参加的概率．
下面的临界值表供参考：
（参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）
某大学为了在2016年全国大学生成语听写大赛取得优秀成绩，抽调男女各20名学生组成集训队进行成语听写集训，集训结束时，为了检验集训效果，对所有集训队员进行成语听写考核，试题为听写100个常用成语（每个1分，满分100分），考核成绩如图茎叶图所示：（I）若大于或等于80分为优秀队员，80分以下为非优秀队员，根据茎叶图填写下面2×2列联表，并判断能否有95%的把握认为队员的优秀与性别有关？
| 非优秀 | 优秀 | 总数 | |
| 男 | 20 | ||
| 女 | 20 | ||
| 总数 | 40 |
下面的临界值表供参考：
| P（K2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
15．
如图所示的程序框图中输入x的值是[1，9]内任取的一个实数，执行该程序，则输出x的值小于55的概率为（ ）
如图所示的程序框图中输入x的值是[1，9]内任取的一个实数，执行该程序，则输出x的值小于55的概率为（ ）| A． | $\frac{3}{8}$ | B． | $\frac{5}{8}$ | C． | $\frac{1}{3}$ | D． | $\frac{2}{3}$ |
2．设p：?x0∈R，mx02+1≤0，q：x∈R，x2+mx+1＞0，若p∨q为真命题，则实数m的取值范围是（ ）
| A． | （-∞，2） | B． | （2，+∞） | C． | （-2，2） | D． | （-∞，2]∪[2，+∞） |
20．函数f（x）=$\frac{1}{3}$ax3+$\frac{1}{2}$ax2-2ax+2a+1的图象经过四个象限的一个充分但不必要条件是（ ）
| A． | -$\frac{4}{3}$＜a＜-$\frac{1}{3}$ | B． | -1＜a＜-$\frac{1}{2}$ | C． | -$\frac{6}{5}$＜a＜-$\frac{3}{16}$ | D． | -2＜a＜0 |