题目内容
11.若函数$f(x)=tan(ωx+\frac{π}{4})(ω>0)$的最小正周期为2π,则ω=$\frac{1}{2}$;$f(\frac{π}{3})$=2+$\sqrt{3}$.分析 直接利用周期公式T=$\frac{π}{|ω|}$,求出实数ω的值,利用特殊角的三角函数值,两角和的正切函数公式即可化简求值.
解答 解:因为函数$f(x)=tan(ωx+\frac{π}{4})(ω>0)$的最小正周期为2π,所以$\frac{π}{|ω|}$=2π,解得:ω=$\frac{1}{2}$.
$f(\frac{π}{3})$=tan($\frac{1}{2}$×$\frac{π}{3}$+$\frac{π}{4}$)=$\frac{tan\frac{π}{6}+tan\frac{π}{4}}{1-tan\frac{π}{6}tan\frac{π}{4}}$=$\frac{\frac{\sqrt{3}}{3}+1}{1-\frac{\sqrt{3}}{3}}$=2+$\sqrt{3}$.
故答案为:$\frac{1}{2}$,2+$\sqrt{3}$.
点评 本题主要考查了正切函数的最小正周期的求法,考查了特殊角的三角函数值,两角和的正切函数公式在三角函数化简求值中的应用,是常考题型,属于基础题.

练习册系列答案
相关题目
1.如图,为一个半圆柱和一个半圆锥拼接而成的组合体的三视图,则该组合体的体积为( )
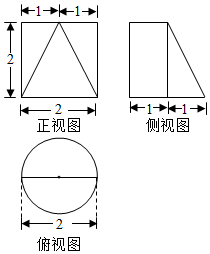

| A. | $\frac{8π}{3}$ | B. | $\frac{4π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}$ |
19.抛物线x2=-2y的焦点坐标为( )
| A. | $(0,-\frac{1}{8})$ | B. | $(-\frac{1}{8},0)$ | C. | $(0,-\frac{1}{2})$ | D. | $(-\frac{1}{2},0)$ |
6.定义集合A?B={x|x∈A或x∈B且x∉A∩B},设全集U={x|1<x<10},集合A={x|2<x<6},B={x|5<x<7},则(∁UA)?B=( )
| A. | [6,7) | B. | (1,2]∪(5,6)∪[7,10) | C. | (1,6) | D. | (1,2]∪(5,6]∪(7,10) |
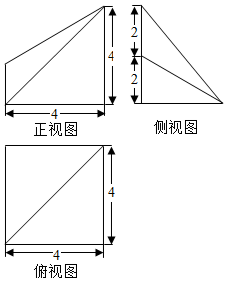 已知某几何体的三视图如图所示,则该几何体的体积为$\frac{80}{3}$.
已知某几何体的三视图如图所示,则该几何体的体积为$\frac{80}{3}$.