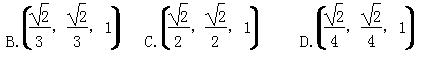题目内容
如图,在四棱锥V-ABCD中,底面ABCD是矩形,侧棱VA⊥底面ABCD,VA=1,E、F、G分别为VA、VB、BC的中点.
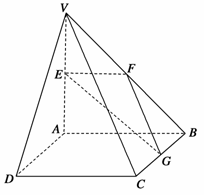
(1)求证:平面EFG∥平面VCD;
(2)当二面角V-BC-A、V-DC-A依次为45°、30°时,求直线VC与平面ABCD所成的角正弦值.
解:
(1)∵E、F、G分别为VA、VB、BC的中点,
∴EF∥AB,FG∥VC,
又ABCD是矩形,∴AB∥CD,∴EF∥CD,
又∵EF⊄平面VCD,FG⊄平面VCD,
∴EF∥平面VCD,FG∥平面VCD,
又EF∩FG=F,∴平面EFG∥平面VCD.
(2)、连接AC,由题意可知:直线VC与平面ABCD所成的角为:∠VCA,
∵二面角V-BC-A、V-DC-A依次为45°、30°
∴∠VBA=45°, ∠VDA=30°
∵VA=1,∴AB=1,AD=
∴AC=2,∴VC=
∴

练习册系列答案
相关题目



 dx=________.
dx=________. 的公比
的公比 ,前
,前 项和为
项和为 ,则
,则 等于( )
等于( ) D、
D、
 上有一点P到左焦点的距离是4,则点p到右焦点的距离是( )
上有一点P到左焦点的距离是4,则点p到右焦点的距离是( ) 且
且 ,则
,则 的最小值为 ( )
的最小值为 ( )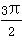 B.
B.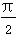 <an+1-an<π
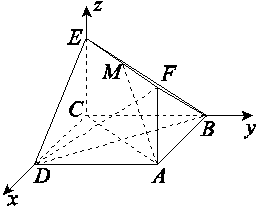
<an+1-an<π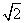 ,AF=1,M在EF上且AM∥平面BDE,则点M的坐标为( )
,AF=1,M在EF上且AM∥平面BDE,则点M的坐标为( )