题目内容
已知函数f(x)=kx2+4x-2在[1,2]上为增函数,求实数k的取值范围.
考点:函数单调性的判断与证明,二次函数的性质
专题:函数的性质及应用
分析:直接分k=0,k>0和k<0讨论,当k<0时由二次函数的对称轴在[1,2]的右端点或其右侧求解.
解答:
解:当k=0时,f(x)=4x-2,满足在[1,2]上为增函数;
当k>0时,函数f(x)=kx2+4x-2的对称轴方程为x=-
<0,函数满足在[1,2]上为增函数;
当k<0时,要使f(x)=kx2+4x-2在[1,2]上为增函数,则-
≥2,即-1≤k<0.
综上,使函数f(x)=kx2+4x-2在[1,2]上为增函数的实数k的取值范围是[-1,+∞).
当k>0时,函数f(x)=kx2+4x-2的对称轴方程为x=-
| 2 |
| k |
当k<0时,要使f(x)=kx2+4x-2在[1,2]上为增函数,则-
| 2 |
| k |
综上,使函数f(x)=kx2+4x-2在[1,2]上为增函数的实数k的取值范围是[-1,+∞).
点评:本题考查了二次函数的单调性,考查了分类讨论的数学思想方法,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
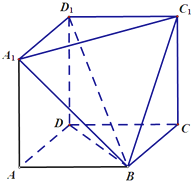 如图,在几何体ABCD-A1D1C1中,四边形ABCD,A1ADD1,DCC1D1均为边长为1的正方形.
如图,在几何体ABCD-A1D1C1中,四边形ABCD,A1ADD1,DCC1D1均为边长为1的正方形.