题目内容
13．在△ABC中，三个内角A、B、C的对边分别是a，b，c，sinA＞sinB则下列结论不一定成立的是（ ）| A． | A＞B | B． | sin2A＞sin2B | C． | cos2A＜cos2B | D． | a＞b |
分析 由题意，利用正弦定理，二倍角公式，依次判断即可．
解答 解：由题意，sinA＞sinB，正弦定理可得，a＞b，A＞B．∴A，D选项正确．
对于B选项：sin2A=2sinAcosA，sin2B=2sinBcosB，
∵π＞A＞B＞0，
设A=60°，B=45°，
则sin2A＜sin2B．故B不对．
对于C：cos2A=1-2sin2A，
cos2B=1-2sin2B，
∵sinA＞sinB＞0
∴cos2A＜cos2B．∴C正确．
故选：B．
点评 本题考查了正弦定理，二倍角公式的灵活运用，比较基础．
练习册系列答案
相关题目
3．为了对某班学生的数学、物理成绩进行分析，从该班25位男同学，15位女同学中随机抽取一个容量为8的样本．
（1）如果按性别比例分层抽样，可以得到多少个不同的样本？（只要求写出算式，不必计算出结果）；
（2）若这8人的数学成绩从小到大排序是65，68，72，79，81，88，92，95．物理成绩从小到大排序是72，77，80，84，86，90，93，98．
①求这8人中恰有3人数学、物理成绩均在85分以上的概率（结果用分数表示）；
②已知随机抽取的8人的数学成绩和物理成绩如表：
若以数学成绩为解释变量x，物理成绩为预报变量y，求y关于x的线性回归方程（系数精确到0.01）；并求数学成绩对于物理成绩的贡献率R2（精确到0.01）．
参考公式：相关系数：r=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sqrt{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}\sum_{i=1}^{n}（{y}_{i}-\overline{y}）^{2}}}$，R2=r2，
回归方程：$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$，其$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$
参考数据：$\overline{x}$=80，$\overline{y}$=85，$\sum_{i=1}^{8}$（xi-$\overline{x}$）2=868，$\sum_{i=1}^{8}$（yi-$\overline{y}$）2═518，$\sum_{i=1}^{8}$（xi-$\overline{x}$）（yi-$\overline{y}$）=664，$\sqrt{868}$≈29.5，$\sqrt{518}$≈22.8．
（1）如果按性别比例分层抽样，可以得到多少个不同的样本？（只要求写出算式，不必计算出结果）；
（2）若这8人的数学成绩从小到大排序是65，68，72，79，81，88，92，95．物理成绩从小到大排序是72，77，80，84，86，90，93，98．
①求这8人中恰有3人数学、物理成绩均在85分以上的概率（结果用分数表示）；
②已知随机抽取的8人的数学成绩和物理成绩如表：
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学成绩 | 65 | 68 | 72 | 79 | 81 | 88 | 92 | 95 |
| 物理成绩 | 72 | 77 | 80 | 84 | 86 | 90 | 93 | 98 |
参考公式：相关系数：r=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sqrt{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}\sum_{i=1}^{n}（{y}_{i}-\overline{y}）^{2}}}$，R2=r2，
回归方程：$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$，其$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$
参考数据：$\overline{x}$=80，$\overline{y}$=85，$\sum_{i=1}^{8}$（xi-$\overline{x}$）2=868，$\sum_{i=1}^{8}$（yi-$\overline{y}$）2═518，$\sum_{i=1}^{8}$（xi-$\overline{x}$）（yi-$\overline{y}$）=664，$\sqrt{868}$≈29.5，$\sqrt{518}$≈22.8．
4．如图是某个几何体的三视图，则该几何体的体积是（ ）
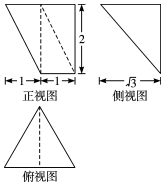
| A． | $\sqrt{3}$ | B． | 2 | C． | 3 | D． | 4 |
8．已知函数f（x）的导函数为f'（x），且$f（1）=\frac{1}{2}$，不等式$f'（x）≤\frac{1}{x}+x$的解集为（0，1]，则不等式$\frac{f（x）-lnx}{x^2}＞\frac{1}{2}$的解集为（ ）
| A． | （0，1） | B． | （0，+∞） | C． | （1，+∞） | D． | （0，1）∪（1，+∞） |