题目内容
2.判断下列命题是全称命题还是特称命题,并用符号“?”或“?”表示下列命题.(1)自然数的平方大于或等于零;
(2)圆x2+y2=1上存在一个点到直线y=x+1的距离等于圆的半径;
(3)有的函数既是奇函数又是增函数;
(4)对于数列{$\frac{n}{n+1}$},总存在正整数n0,使得a${\;}_{{n}_{0}}$与1之差的绝对值小于0.01.
分析 由全称命题与特称命题的概念,包含所有,任意的…等全称量词的命题都是全称命题,有些命题隐藏了全称量词,但是仍然是全称命题,要具体分析.含有存在、有一个…等存在量词的命题为特称命题,由此对四个答案进行分析,即可得到答案.
解答 (1)命题可以补充为:所有自然数的平方大于或等于零,故这是全称命题;
(2)命题含有量词“存在”,是特称命题;
(3)命题含有存在量词“有的”,是特称命题;
(4)命题的含义是“对于数列{$\frac{n}{n+1}$},总存在正整数n0,使得a${\;}_{{n}_{0}}$与1之差的绝对值小于0.01”
点评 本题考查的知识点是全称命题和特称命题的定义,熟练掌握全称命题和特称命题的定义是解答本题的关键.

练习册系列答案
相关题目
14.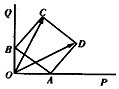 如图,边长为2的正方形 A BCD的顶点 A,B分别在两条互相垂直的射线 OP,OQ上滑动,则$\overrightarrow{{O}C}•\overrightarrow{{O}D}$的最大值为( )
如图,边长为2的正方形 A BCD的顶点 A,B分别在两条互相垂直的射线 OP,OQ上滑动,则$\overrightarrow{{O}C}•\overrightarrow{{O}D}$的最大值为( )
 如图,边长为2的正方形 A BCD的顶点 A,B分别在两条互相垂直的射线 OP,OQ上滑动,则$\overrightarrow{{O}C}•\overrightarrow{{O}D}$的最大值为( )
如图,边长为2的正方形 A BCD的顶点 A,B分别在两条互相垂直的射线 OP,OQ上滑动,则$\overrightarrow{{O}C}•\overrightarrow{{O}D}$的最大值为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
12.已知函数f(x)的导函数f′(x),满足(x-2)[f′(x)-f(x)]>0,且f(4-x)=e4-2xf(x),则下列关于
f(x)的命题正确的是( )
f(x)的命题正确的是( )
| A. | f(3)>e2f(1) | B. | f(3)<ef(2) | C. | f(4)<e4f(0) | D. | f(4)<e5f(-1) |