题目内容
14.已知${({\frac{1}{{2\sqrt{x}}}+2x})^n}(n∈{N^*})$展开式中第6项为常数.(1)求n的值;
(2)求展开式中系数最大项.
分析 (1)根据通项公式即可求出n的值,
(2)设展开式系数最大项为第r+1项,则得到关于r烦人不等式组,解得r,问题得以解决
解答 解:(1)展开式的通项公式为 Tr+1=2-n+2r•Cnrx${\;}^{\frac{n-3r}{2}}$,
∵展开式中第6项为常数,
∴r=5,
即为$\frac{n-15}{2}$=0,
解得n=15,
(2)设展开式系数最大项为第r+1项,则有2-15+2r•C15r≥2-13+2r•C15r+1,
2-15+2r•C15r≤2-17+2r•C15r-1,
解得r=12
故第13项的系数最大为2-15+24•C1512x${\;}^{\frac{15-3×12}{2}}$=29C153x${\;}^{-\frac{21}{2}}$
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于中档题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
13.已知数列{an}的通项公式为${a_n}=lg\frac{{{n^2}+3n+2}}{{{n^2}+3n}},n∈{N^*}$,则数列{an}的前n项和Sn=( )
| A. | $lg\frac{3}{n+3}$ | B. | $lg\frac{2}{n}$ | C. | $lg\frac{{3({n+1})}}{n+3}$ | D. | $lg\frac{{2({n+2})}}{n}$ |
2.若a-b>0,下列不等式一定成立的个数是( )
(1)$\frac{1}{a}<\frac{1}{b}$(2)$\frac{b}{a}<1$(3)2a-b>1(4)ln(a-b)>0.
(1)$\frac{1}{a}<\frac{1}{b}$(2)$\frac{b}{a}<1$(3)2a-b>1(4)ln(a-b)>0.
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
19.已知回归方程为:$\widehat{y}$=3-2x,若解释变量增加1个单位,则预报变量平均( )
| A. | 增加2个单位 | B. | 减少2个单位 | C. | 增加3个单位 | D. | 减少3个单位 |
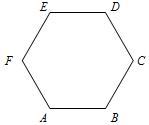 如图,点P是边长为1的正六边形ABCDEF的边上的一个动点,设$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AE}$,则x+y的最大值为2.
如图,点P是边长为1的正六边形ABCDEF的边上的一个动点,设$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AE}$,则x+y的最大值为2.