题目内容
若数列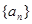 满足
满足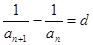 (其中d为常数,
(其中d为常数,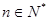 ),则称数列
),则称数列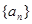 为“调和数列”,已知数列
为“调和数列”,已知数列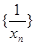 为调和数列,且
为调和数列,且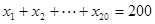 ,则
,则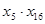 的最大值为 .
的最大值为 .
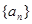 满足
满足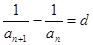 (其中d为常数,
(其中d为常数,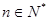 ),则称数列
),则称数列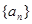 为“调和数列”,已知数列
为“调和数列”,已知数列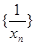 为调和数列,且
为调和数列,且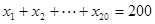 ,则
,则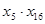 的最大值为 .
的最大值为 .100.
试题分析:因为数列
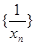 为“调和数列”,所以xn+1-xn=d(n∈N*,d为常数),即数列{xn}为等差数列,由x1+x2+…+x20=200得
为“调和数列”,所以xn+1-xn=d(n∈N*,d为常数),即数列{xn}为等差数列,由x1+x2+…+x20=200得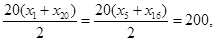 即
即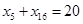 ,
,易知x3、x18都为正数时,x3x18取得最大值,所以
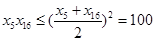 ,即
,即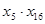 的最大值为100.
的最大值为100.点评:解本小题关键是根据因为数列
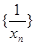 为“调和数列”,得到{xn}为等差数列,然后再解题的过程中利用性质:若
为“调和数列”,得到{xn}为等差数列,然后再解题的过程中利用性质:若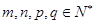 ,则
,则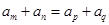 ,得到
,得到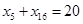 ,然后使用基本不等式求出
,然后使用基本不等式求出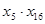 的最值.
的最值. 
练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
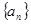 满足
满足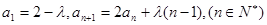
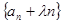 为等比数列;
为等比数列;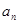 以及前n项和
以及前n项和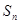 ;
;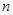 都有
都有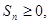 求
求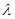 的取值范围。
的取值范围。 =
= 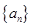 是等差数列,其中
是等差数列,其中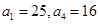 .
.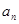 ;
;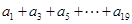 值.
值.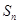 表示等差数列
表示等差数列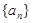 的前
的前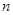 项和,且
项和,且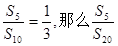 等于( )
等于( )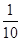
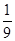
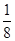
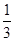
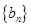 的前
的前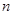 项和为
项和为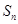 ,且
,且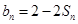 ;数列
;数列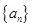 为等差数列,且
为等差数列,且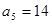 ,
,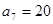 .
.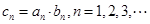 ,
,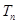 为数列
为数列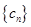 的前
的前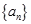 的前n项和为
的前n项和为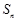 ,且满足
,且满足 ,
, =1,2,3,….
=1,2,3,….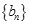 满足
满足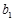 =1,且
=1,且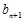 =
=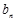 +
+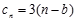 ,求数列
,求数列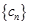 的前
的前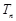 .
.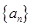 的前
的前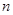 项和为
项和为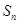 ,且
,且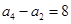 ,
,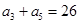 ,记
,记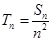 ,如果存在正整数
,如果存在正整数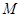 ,使得对一切正整数
,使得对一切正整数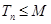 都成立,则
都成立,则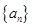 是首项为
是首项为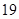 ,公差为
,公差为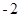 的等差数列.
的等差数列.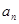 ;
; 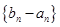 是首项为
是首项为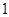 ,公比为
,公比为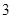 的等比数列,求数列
的等比数列,求数列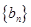 的通项公式及其前
的通项公式及其前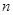 项和
项和 .
.