题目内容
已知双曲线的左右焦点分别为F1(-4,0),F2(4,0),且点P(4,6)在双曲线上,求双曲线的方程.
考点:双曲线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:根据焦点为F1(-4,0)、F2(4,0),且经过点(4,6)求出双曲线的几何量,即可得出双曲线的标准方程.
解答:
解:依题意得,双曲线的中心在原点,焦点为F1(-4,0)、F2(4,0),
∴c=4,
又点P(4,6)在双曲线上,
∴2a=|
-
|=4,
∴a=2,
∴b2=c2-a2=12,
∵双曲线焦点在焦点在x轴上,
∴双曲线的标准方程为:
-
=1
∴c=4,
又点P(4,6)在双曲线上,
∴2a=|
| (4+4)2+62 |
| (4-4)2+62 |
∴a=2,
∴b2=c2-a2=12,
∵双曲线焦点在焦点在x轴上,
∴双曲线的标准方程为:
| x2 |
| 4 |
| y2 |
| 12 |
点评:本题考查双曲线标准方程的求法,双曲线的简单性质,关键是a,b的求法,是中档题.

练习册系列答案
相关题目
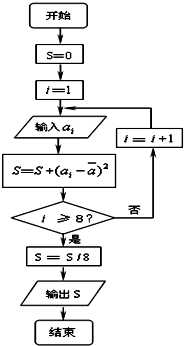 对一个作直线运动的质点的运动过程观测了8次,第i次观测得到的数据为
对一个作直线运动的质点的运动过程观测了8次,第i次观测得到的数据为ai,具体如表所示:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| ai | 40 | 41 | 43 | 43 | 44 | 46 | 47 | 48 |
. |
| a |
| A、5 | B、7 | C、40 | D、56 |
以双曲线
-
=1的离心率为首项,
的公比的等比数列的前n项和Sn( )
| x2 |
| 4 |
| y2 |
| 5 |
| 1 |
| 2 |
A、3(2n-1)-
| ||
B、3-
| ||
C、
| ||
D、
|