题目内容
将并排的有不同编号的5个房间安排给5个工作人员临时休息，假定每个人可以选择任一房间，且选择各个房间是等可能的，则恰有两个房间无人选择且这两个房间不相邻的安排方式的总数为（ ）
| A、900 | B、1500 |
| C、1800 | D、1440 |
考点：计数原理的应用
专题：应用题,排列组合
分析：先从5个房间中任选3个安排给5个工作人员临时休息，这三个房间每个房间都有人，5个人分两组（1，2，2）和（1，1，3）然后再安排房间，问题得以解决．
解答：
解：先从5个房间中任选3个安排给5个工作人员临时休息有
=10种，其中相邻的有4种，故选的房间的种数为10-4=6种，
5个人分两组（1，1，3）和（1，2，2）有
+
=25种分法，然后再全排有
=6种，
故若恰有2个房间无人选择且这2个房间不相邻，则不同的安排方式的总数为6×25×6=900种．
故选：A．
| C | 3 5 |
5个人分两组（1，1，3）和（1，2，2）有
| ||||
|
| ||||
|
| A | 3 3 |
故若恰有2个房间无人选择且这2个房间不相邻，则不同的安排方式的总数为6×25×6=900种．
故选：A．
点评：本题主要考查了排列组合中分组问题，关键是求出5个人分组的种数，属于中档题．
练习册系列答案
课时训练江苏人民出版社系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
数列{an}满足：a1a2a3…an=
，则a2013=（ ）
| 1 |
| n |
A、
| ||
B、
| ||
C、
| ||
D、
|
设f（x）=
x3+ax2+5x+6在区间[1，3]上单调函数，则实数a的取值范围为（ ）
| 1 |
| 3 |
A、[-
| ||
| B、（-∞，-3] | ||
C、[-3，
| ||
D、（-∞，-3]∪[-
|
已知实数a，b满足a2+b2=1，则a4+ab+b4的最小值为（ ）
A、-
| ||
| B、0 | ||
| C、1 | ||
D、
|
在△ABC中，
=
，
=
，D为BC的中点，则
为（ ）
| AB |
| a |
| AC |
| b |
| AD |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
点A（1，0）到直线x+y-2=0的距离为（ ）
A、
| ||||
B、
| ||||
| C、1 | ||||
| D、2 |
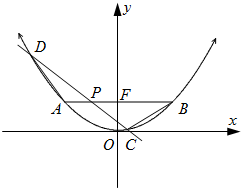如图，已知抛物线M的参数方程为
已知E、F、G、H分别是四面体ABCD的棱AD、CD、BD、BC的中点．求证：AH∥平面EFG．