题目内容
18.已知函数f(x)=$\frac{1}{3}$x3-bx+c(b,c∈R).(1)若函数f(x)在点(1,f(1))处的切线方程为y=2x+1,求b,c的值;
(2)若b=1,函数f(x)在区间(0,2)内有唯一零点,求c的取值范围.
分析 (1)求导数,利用导数的几何意义及切点坐标,求b,c的值;
(2)f(x)在(0,1)上单调递减,在(1,2)上单调递增,又$f(0)=c<f(2)=\frac{2}{3}+c$,可知f(x)在区间(0,2)内有唯一零点等价于f(1)=0或$\left\{{\begin{array}{l}{f(0)≤0}\\{f(2)>0}\end{array}}\right.$,即可求c的取值范围.
解答 解:(1)f′(x)=x2-b,所以f′(1)=1-b=2,得b=-1
又f(1)=2+1=3,所以$\frac{1}{3}-b+c=3$,得$c=\frac{5}{3}$(3分)
(2)因为b=1所以$f(x)=\frac{1}{3}{x^3}-x+c$,f′(x)=x2-1.
当x∈(0,1)时,f′(x)<0,当x∈(1,2)时,f′(x)>0,
所以f(x)在(0,1)上单调递减,在(1,2)上单调递增
又$f(0)=c<f(2)=\frac{2}{3}+c$,可知f(x)在区间(0,2)内有唯一零点等价于f(1)=0或$\left\{{\begin{array}{l}{f(0)≤0}\\{f(2)>0}\end{array}}\right.$,
得$c=\frac{2}{3}$或$-\frac{2}{3}<c≤0$(9分)
点评 本题考查函数的导数的综合应用,函数的单调性以及导数的几何意义,考查分析问题解决问题的能力.

练习册系列答案
相关题目
6.在极坐标系中,圆心在($\sqrt{2}$,π)且过极点的圆的方程为( )
| A. | ρ=2$\sqrt{2}$cos θ | B. | ρ=-2$\sqrt{2}$cos θ | C. | ρ=2$\sqrt{2}$sin θ | D. | ρ=-2$\sqrt{2}$sin θ |
13.若关于x的不等式|x+3|-|x-1|>a2-3a的解集不空,则实数a的范围是( )
| A. | (-∞,-1)∪(4,+∞) | B. | (-1,4) | C. | (-∞,-4)∪(1,+∞) | D. | (-4,1) |
3.已知向量$\overrightarrow a$=(x,1),$\overrightarrow b$=(1,-1),若$\overrightarrow a$∥$\overrightarrow b$,则x=( )
| A. | -1 | B. | 1 | C. | ±1 | D. | 0 |
10.有5名同学站成一排照相,则甲与乙相邻的不同排法种数有( )
| A. | 8 | B. | 12 | C. | 36 | D. | 48 |
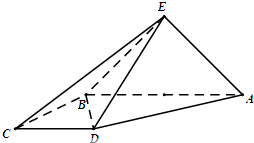 如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直.AB∥CD,AB⊥BC,AB=2CD=2BC=2,EA⊥EB.
如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直.AB∥CD,AB⊥BC,AB=2CD=2BC=2,EA⊥EB.