题目内容
某校卫生所成立了调查小组,调查“按时刷牙与患龋齿的关系”,对该校某年级700名学生进行检查,按患龋齿和不患龋齿分类,得汇总数据:按时刷牙且不患龋齿的学生有60名,不按时刷牙但不患龋齿的学生有100名,按时刷牙但患龋齿的学生有140名.
(1)能否在犯错概率不超过0.01的前提下,认为该年级学生的按时刷牙与患龋齿有关系?
(2)4名校卫生所工作人员甲、乙、丙、丁被随机分成两组,每组2人,一组负责数据收集,
另一组负责数据处理,求工作人员甲分到“负责收集数据组”并且工作人员乙分到“负责数据处理组”的概率.
附:k2=
?
(1)能否在犯错概率不超过0.01的前提下,认为该年级学生的按时刷牙与患龋齿有关系?
(2)4名校卫生所工作人员甲、乙、丙、丁被随机分成两组,每组2人,一组负责数据收集,
另一组负责数据处理,求工作人员甲分到“负责收集数据组”并且工作人员乙分到“负责数据处理组”的概率.
附:k2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.010 | 0.005 | 0.001 |
| K0 | 6.635 | 7.879 | 10.828 |
考点:独立性检验
专题:概率与统计
分析:(1)根据题意,列出2×2联表,计算k2的值,判断是否在犯错误率不超过0.01的前提下,认为该年级学生按时刷牙与患龋齿有关系即可;
(2)列出4人分组的所有情况,求出 对应的概率是多少.
(2)列出4人分组的所有情况,求出 对应的概率是多少.
解答:
解:(1)根据题意,列2×2联表如下,
因为k2=
≈8.102>6.635,
所以能在犯错误率不超过0.01的前提下,认为该年级学生按时刷牙与患龋齿有关系;
(2)4人分组的所有情况如下表;
分组的情况共有6种,工作人员甲负责收集数据且工作人员乙负责处理数据有2种,
所以工作人员甲负责收集数据且工作人员处理数据的概率是P=
=
.
| 按时刷牙 | 不按时刷牙 | 总计 | |
| 不患龋齿 | 60 | 100 | 160 |
| 患龋齿 | 140 | 400 | 540 |
| 总计 | 200 | 500 | 700 |
| 700(60×400-100×140)2 |
| 160×540×200×500 |
所以能在犯错误率不超过0.01的前提下,认为该年级学生按时刷牙与患龋齿有关系;
(2)4人分组的所有情况如下表;
| 小组 | 1 | 2 | 3 | 4 | 5 | 6 |
| 收集数据 | 甲乙 | 甲丙 | 甲丁 | 乙丙 | 乙丁 | 丙丁 |
| 处理数据 | 丙丁 | 乙丁 | 乙丙 | 甲丁 | 甲丙 | 甲乙 |
所以工作人员甲负责收集数据且工作人员处理数据的概率是P=
| 2 |
| 6 |
| 1 |
| 3 |
点评:本题考查了独立性检验的与概率的计算问题,解题时应根据题目中的计算公式进行计算,是基础题目.

练习册系列答案
相关题目
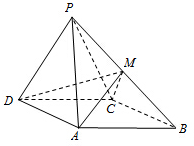 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ADC=60°,侧面PDC是正三角形,平面PDC⊥平面ABCD,CD=2,M为PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ADC=60°,侧面PDC是正三角形,平面PDC⊥平面ABCD,CD=2,M为PB的中点.
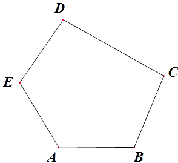 如图所示,一个确定的凸五边形 ABCDE,令x=
如图所示,一个确定的凸五边形 ABCDE,令x=