题目内容
已知函数f(x)=
(其中k∈R,e=2.71828…是自然数的底数),f′(x)为f(x)的导函数.
(1)当k=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若x∈(0,1]时,f′(x)=0都有解,求k的取值范围;
(3)若f′(1)=0,试证明:对任意x>0,f′(x)<
恒成立.
| lnx+k |
| ex |
(1)当k=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若x∈(0,1]时,f′(x)=0都有解,求k的取值范围;
(3)若f′(1)=0,试证明:对任意x>0,f′(x)<
| e-2+1 |
| x2+x |
考点:利用导数研究曲线上某点切线方程,导数在最大值、最小值问题中的应用
专题:导数的概念及应用,导数的综合应用,不等式的解法及应用
分析:(1)求出当k=2时,f(x)的导数,求得切线的斜率和切点,由点斜式方程即可得到切线方程;
(2)由f′(x)=0可得k=
,运用导数求得右边函数的最大值,即可得到k的范围;
(3)由f′(1)=0,可得k=1,对任意x>0,g(x)<e-2+1等价为1-x-xlnx<
(e-2+1),先证1-x-xlnx≤e-2+1,可由导数求得,再证
>1.即可证得对任意x>0,f′(x)<
恒成立.
(2)由f′(x)=0可得k=
| 1-xlnx |
| x |
(3)由f′(1)=0,可得k=1,对任意x>0,g(x)<e-2+1等价为1-x-xlnx<
| ex |
| x+1 |
| ex |
| x+1 |
| e-2+1 |
| x2+x |
解答:
解:(1)当k=2时,f(x)=
的导数为f′(x)=
(x>0),
f′(1)=-
,f(1)=
,在点(1,f(1))处的切线方程为y-
=-
(x-1),
即为y=-
x+
;
(2)f′(x)=0,即
=0,即有k=
,
令F(x)=
,由0<x≤1,F′(x)=-
<0,
F(x)在(0,1)递减,x→0,F(x)→+∞,F(x)≤1,
即k≤1;
(3)证明:由f′(1)=0,可得k=1,g(x)=(x2+x)f′(x),即g(x)=
(1-x-xlnx),
对任意x>0,g(x)<e-2+1等价为1-x-xlnx<
(e-2+1),
由h(x)=1-x-xlnx得h′(x)=-2-lnx,
当0<x<e-2时,h′(x)>0,h(x)递增,当x>e-2时,h′(x)<0,h(x)递减,
则h(x)的最大值为h(e-2)=1+e-2,故1-x-xlnx≤e-2+1,
设φ(x)=ex-(x+1),φ′(x)=ex-1,x>0时,φ′(x)>0,φ(x)>0,
φ(x)>φ(0)=0,则x>0时,φ(x)=ex-(x+1)>0即
>1.
即1-x-xlnx≤e-2+1<
(e-2+1),
故有对任意x>0,f′(x)<
恒成立.
| lnx+2 |
| ex |
| 1-2x-xlnx |
| xex |
f′(1)=-
| 1 |
| e |
| 2 |
| e |
| 2 |
| e |
| 1 |
| e |
即为y=-
| 1 |
| e |
| 3 |
| e |
(2)f′(x)=0,即
| 1-kx-xlnx |
| xex |
| 1-xlnx |
| x |
令F(x)=
| 1-xlnx |
| x |
| x+1 |
| x2 |
F(x)在(0,1)递减,x→0,F(x)→+∞,F(x)≤1,
即k≤1;
(3)证明:由f′(1)=0,可得k=1,g(x)=(x2+x)f′(x),即g(x)=
| x+1 |
| ex |
对任意x>0,g(x)<e-2+1等价为1-x-xlnx<
| ex |
| x+1 |
由h(x)=1-x-xlnx得h′(x)=-2-lnx,
当0<x<e-2时,h′(x)>0,h(x)递增,当x>e-2时,h′(x)<0,h(x)递减,
则h(x)的最大值为h(e-2)=1+e-2,故1-x-xlnx≤e-2+1,
设φ(x)=ex-(x+1),φ′(x)=ex-1,x>0时,φ′(x)>0,φ(x)>0,
φ(x)>φ(0)=0,则x>0时,φ(x)=ex-(x+1)>0即
| ex |
| x+1 |
即1-x-xlnx≤e-2+1<
| ex |
| x+1 |
故有对任意x>0,f′(x)<
| e-2+1 |
| x2+x |
点评:本题考查导数的运用:求切线方程和单调区间及极值、最值,运用分离参数和不等式恒成立问题转化为不等式的传递性是解题的关键.

练习册系列答案
相关题目
下列4个正方体图形中,l是正方体的一条对角线,点M、N、P分别为其所在棱的中点,能得出直线l⊥面MNP的所有图形的序号是( )
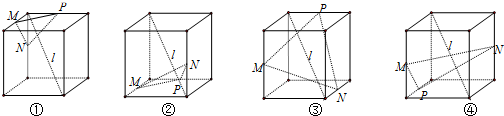

| A、①④ | B、①② | C、②④ | D、①③ |
已知凼数F(x)为二次凼数,且F(x)的导凼数为f(x),若存在实数a∈(-2,-1),使f(-a)=-f(a)>0,则不等式F(2x-1)>F(x)的解集为( )
A、{x|x<
| ||
B、{x|x<
| ||
C、{x|
| ||
D、{x|x<-1或x>-
|
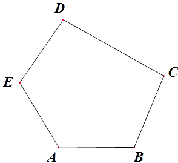 如图所示,一个确定的凸五边形 ABCDE,令x=
如图所示,一个确定的凸五边形 ABCDE,令x=