题目内容
若
≠kx+2对一切x≥5都成立,则k的取值范围是 .
| x-5 |
考点:函数恒成立问题
专题:数形结合
分析:分别作出不等式两边所对应的函数的图象,由图象可知k=0不满足题意,k<0时直线y=kx+2的斜率应小于过两点(5,0)和(0,2)的直线的斜率,k>0时联立直线和抛物线方程,由判别式小于0得答案.
解答:
解:令y=
,得y2=x-5(y≥0),
∴函数y=
的图象如图,
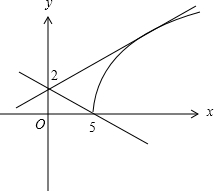
又函数y=kx+2恒过定点(0,2),
k=0时显然不满足题意;
∴当k<0时,要使
≠kx+2对一切x≥5都成立,则k<-
;
当k>0时,联立
,得k2x2+(4k-1)x+9=0(x≥5).
由△=(4k-1)2-36k2<0,得k<-
(舍),或k>
.
综上,实数k的取值范围是,k<-
或k>
.
故答案为:k<-
或k>
.
| x-5 |
∴函数y=
| x-5 |

又函数y=kx+2恒过定点(0,2),
k=0时显然不满足题意;
∴当k<0时,要使
| x-5 |
| 2 |
| 5 |
当k>0时,联立
|
由△=(4k-1)2-36k2<0,得k<-
| 1 |
| 2 |
| 1 |
| 10 |
综上,实数k的取值范围是,k<-
| 2 |
| 5 |
| 1 |
| 10 |
故答案为:k<-
| 2 |
| 5 |
| 1 |
| 10 |
点评:本题考查了函数恒成立问题,考查了数形结合的解题思想方法和数学转化思想方法,是中档题.

练习册系列答案
相关题目
动点P(m,n)到直线l:x=-5的距离为λ
,点P的轨迹为双曲线(且原点O为准线l对应的焦点),则λ的取值为( )
| m2+n2 |
| A、λ∈R | B、λ=1 |
| C、λ>1 | D、0<λ<1 |
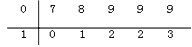 如图所示的茎叶图记录了一组数据,关于这组数据给出了如下四个结论:①众数是9;②平均数10;③中位数是9或10;④方差是3.4,其中正确命题的个数是( )
如图所示的茎叶图记录了一组数据,关于这组数据给出了如下四个结论:①众数是9;②平均数10;③中位数是9或10;④方差是3.4,其中正确命题的个数是( )