题目内容
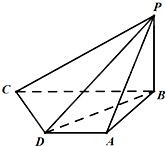如图所示，已知四棱锥P-ABCD中，底面ABCD是直角梯形，AD∥BC，AB⊥BC，AB=AD=1，BC=2，PB⊥平面ABCD，PB=1．（1）求异面直线PA与CD所成角的大小；
（2）求二面角A-PD-B的大小．
考点：二面角的平面角及求法,异面直线及其所成的角
专题：空间角
分析：（1）取BC中点F，连结AF交BD于E，连结PF，∠FAP是异面直线PA与CD所成的角，由此能求出异面直线PA与CD所成角．
（2）连结AF，交BD于E，过E作EG⊥PD于G，连结AG，由已知得∠AGE为二面角A-PD-B的平面角，由此能求出二面角A-PD-B的大小．
（2）连结AF，交BD于E，过E作EG⊥PD于G，连结AG，由已知得∠AGE为二面角A-PD-B的平面角，由此能求出二面角A-PD-B的大小．
解答：
解：（1）取BC中点F，连结AF交BD于E，连结PF，
在梯形ABCD中，AF∥CD，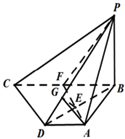
∴∠FAP是异面直线PA与CD所成的角，
在△PFA中，AF=
，PF=
，PA=
，
∴∠PFA=
，
∴异面直线PA与CD所成角为
．
（2）连结AF，交BD于E，过E作EG⊥PD于G，连结AG，
∵PB⊥平面ABCD，∴平面PBD⊥平面ABCD，
在菱形ABFD中，AE⊥BD，则AE⊥平面PBD，
∵EG⊥PD，∴AG⊥PD，
∴∠AGE为二面角A-PD-B的平面角，
在△AGE中，AE=
，EG=
，
∴tan∠AGE=
=
，
∴∠AGE=
，
∴二面角A-PD-B的大小为
．
在梯形ABCD中，AF∥CD，
∴∠FAP是异面直线PA与CD所成的角，
在△PFA中，AF=
| 2 |
| 2 |
| 2 |
∴∠PFA=
| π |
| 3 |
∴异面直线PA与CD所成角为
| π |
| 3 |
（2）连结AF，交BD于E，过E作EG⊥PD于G，连结AG，
∵PB⊥平面ABCD，∴平面PBD⊥平面ABCD，
在菱形ABFD中，AE⊥BD，则AE⊥平面PBD，
∵EG⊥PD，∴AG⊥PD，
∴∠AGE为二面角A-PD-B的平面角，
在△AGE中，AE=
| ||
| 2 |
| ||
| 6 |
∴tan∠AGE=
| AE |
| EG |
| 3 |
∴∠AGE=
| π |
| 3 |
∴二面角A-PD-B的大小为
| π |
| 3 |
点评：本题考查异面直线所成角的大小的求法，考查二面角的大小的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
命题“存在x0∈R，ex0≤0”的否定是（ ）
| A、不存在x0∈R，ex0＞0 |
| B、存在x0∈R，ex0≥0 |
| C、对任意的x∈R，ex＞0 |
| D、对任意的x∈R，ex≤0 |
